题目内容
1.如果二次函数y=(m-1)x2+2x+1与x轴有两个不同的交点,那么m的取值范围是( )| A. | m>2 | B. | m<2 | C. | m>2且m≠1 | D. | m<2且m≠1 |
分析 根据二次函数的定义和△=b2-4ac>0时,抛物线与x轴有2个交点得到$\left\{\begin{array}{l}{m-1≠0}\\{△={2}^{2}-4(m-1)>0}\end{array}\right.$,然后解不等式组即可.
解答 解:根据题意得$\left\{\begin{array}{l}{m-1≠0}\\{△={2}^{2}-4(m-1)>0}\end{array}\right.$,解得m<2且m≠1.
故选D.
点评 本题考查了抛物线与x轴的交点:对于抛物线y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数,当△=b2-4ac>0时,抛物线与x轴有2个交点;当△=b2-4ac=0时,抛物线与x轴有1个交点;当△=b2-4ac<0时,抛物线与x轴没有交点.记住不要忘了二次项系数不为0.

练习册系列答案
相关题目
17.统计某班40名学生每天从家到学校所需时间如下:
该班级学生从家到学校所需时间的众数为20分,中位数为20分,平均数为21.75分.
| 时间/min | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
| 人数 | 1 | 2 | 5 | 15 | 10 | 5 | 2 |
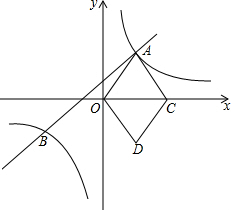 如图,在平面直角坐标系xOy中,直线y=mx+n与双曲线y=$\frac{k}{x}$(k>0)相交于点A、B,点C在x轴正半轴上,点B(-3,-2),D(2,-3),连结OA、OD、DC、AC,四边形AODC为菱形.
如图,在平面直角坐标系xOy中,直线y=mx+n与双曲线y=$\frac{k}{x}$(k>0)相交于点A、B,点C在x轴正半轴上,点B(-3,-2),D(2,-3),连结OA、OD、DC、AC,四边形AODC为菱形.