题目内容
17．
如图，一次函数的y=kx+b图象经过A（2，4）、B（0，2）两点，与x轴交于点C，则△AOC的面积为4．
分析 由图可知A、B两点的坐标，把两点坐标代入一次函数y=kx+b即可求出一次函数的解析式，令y=0，则x=-2，求得C（-2，0），由C点坐标可求出OC的长再由A点纵坐标，利用三角形的面积公式即可得出结论．
解答 解：∵一次函数的y=kx+b图象经过A（2，4）、B（0，2）两点，
∴$\left\{\begin{array}{l}{2k+b=4}\\{b=2}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$，
故此一次函数的解析式为：y=x+2；
令y=0，则x=-2，
∴C（-2，0），
∴OC=2，
∴S△AOC=$\frac{1}{2}$OC•|yA|=$\frac{1}{2}$×2×4=4．
故答案为4．
点评 本题考查的是待定系数法求一次函数的解析式及一次函数图象上点的坐标特点，先根据A、B点的坐标求得解析式是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，DE∥AC，且∠1=∠2，试判断∠ADC与∠FGC有怎样的大小关系？并说明理由．
5．下列计算正确的是（ ）
| A． | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | B． | $3\sqrt{2}-2\sqrt{2}=1$ | C． | $\sqrt{3^2}=3$ | D． | $\sqrt{9}=±3$ |
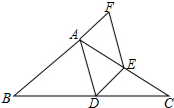如图，△ABC中，点D，E分别是边BC，AC的中点，连接DE，AD，点F在BA的延长线上，且AF=$\frac{1}{2}$AB，连接EF，判断四边形ADEF的形状，并加以证明．