题目内容
4. 如图,在直角坐标系中,A、B的坐标分别为(4,0),(0,2),将线段AB向上平移m个单位得到A′B′,如果△OA′B′为等腰三角形,那么m的值为2或3或2$\sqrt{5}$-2.
如图,在直角坐标系中,A、B的坐标分别为(4,0),(0,2),将线段AB向上平移m个单位得到A′B′,如果△OA′B′为等腰三角形,那么m的值为2或3或2$\sqrt{5}$-2.
分析 根据A、B的坐标分别为(4,0),(0,2),得到OA=4,OB=2,根据勾股定理得到AB=2$\sqrt{5}$,由将线段AB向上平移m个单位得到A′B′,得到A′B′=2$\sqrt{5}$,根据△OA′B′为等腰三角形,①当OB′=A′B′=2$\sqrt{5}$时,②当OA′=A′B′=2$\sqrt{5}$时,③当OB′=A′O=2+m时,分别求得m的值即可.
解答 解:∵A、B的坐标分别为(4,0),(0,2),
∴OA=4,OB=2,
∴AB=2$\sqrt{5}$,
∵将线段AB向上平移m个单位得到A′B′,
∴A′B′=2$\sqrt{5}$,
∵△OA′B′为等腰三角形,
∴①当OB′=A′B′=2$\sqrt{5}$时,
∴m=BB′=2$\sqrt{5}$-2;
②当OA′=A′B′=2$\sqrt{5}$时,m=AA′=2,
③当OB′=A′O=2+m时,
∴2+m=$\sqrt{{4}^{2}+{m}^{2}}$,
∴m=3,
综上所述,如果△OA′B′为等腰三角形,那么m的值为2或3或2$\sqrt{5}$-2.
故答案为:2或3或2$\sqrt{5}$-2.
点评 此题主要考查了坐标与图形的变化--平移,关键是掌握点的坐标的变化规律.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
14.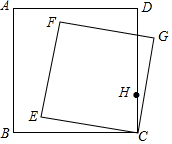 如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )
如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )
 如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )
如图,正方形ABCD中,AB=4,点H在CD边上,且CH=1,点E绕点B旋转,同时,以CE为边在BC上方作正方形CEFG,在点E运动过程中,当线段FH取得最小值时,∠CBE的正切为( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{2}}{5}$ | C. | $\frac{\sqrt{2}}{7}$ | D. | $\frac{1}{7}$ |




 已知:如图,△ABC中,AB=4,AC=6,AD平分∠BAC,且BD⊥AD于D,交AC于F,E是BC的中点,连接DE.求:DE的长度.
已知:如图,△ABC中,AB=4,AC=6,AD平分∠BAC,且BD⊥AD于D,交AC于F,E是BC的中点,连接DE.求:DE的长度.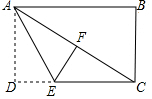 如图,在矩形ABCD中,将△ADE沿AE折叠,点D刚好落在对角线AC上的F点.
如图,在矩形ABCD中,将△ADE沿AE折叠,点D刚好落在对角线AC上的F点.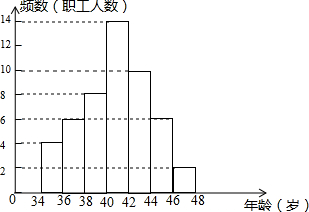 如图是某单位职工年龄(取正整数)的频数分布直方图(每组数据含最小值,不含最大值),则职工人数最多年龄段的职工人数占总人数的百分比为28%.
如图是某单位职工年龄(取正整数)的频数分布直方图(每组数据含最小值,不含最大值),则职工人数最多年龄段的职工人数占总人数的百分比为28%.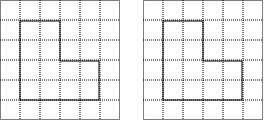 如图所示,在正方形网格中,要求用一条直线将其分成面积相等的两部分,请你设计两种不同的分割方案(用铅笔画图,不写画法,仅用有刻度的直尺,保留作图痕迹或必要的文字说明).
如图所示,在正方形网格中,要求用一条直线将其分成面积相等的两部分,请你设计两种不同的分割方案(用铅笔画图,不写画法,仅用有刻度的直尺,保留作图痕迹或必要的文字说明). 如图,已知AB∥CD,∠1=∠2,那么AE与DF平行吗?试说明理由.
如图,已知AB∥CD,∠1=∠2,那么AE与DF平行吗?试说明理由. 如图,已知EF∥BC,且∠EFD=∠B,请你判断DF与AB的位置关系,并说明理由.
如图,已知EF∥BC,且∠EFD=∠B,请你判断DF与AB的位置关系,并说明理由.