题目内容
19.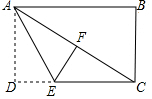 如图,在矩形ABCD中,将△ADE沿AE折叠,点D刚好落在对角线AC上的F点.
如图,在矩形ABCD中,将△ADE沿AE折叠,点D刚好落在对角线AC上的F点.(1)若AB=8,BC=6,求DE的长;
(2)若AE=EC,求证:AC=2BC.
分析 (1)由四边形ABCD是矩形,得到AD=BC=6,CD=AB=8,∠D=∠B=90°,根据勾股定理得到AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=10,根据折叠的性质得到AF=AD=6,DE=EF,根据勾股定理即可得到结论;
(2)根据折叠的性质得到AF=AD,∠AFE=∠D=90°,根据等腰三角形的性质得到AF=CF,于是得到结论.
解答  解:(1)∵四边形ABCD是矩形,
解:(1)∵四边形ABCD是矩形,
∴AD=BC=6,CD=AB=8,∠D=∠B=90°,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=10,
∵将△ADE沿AE折叠,点D刚好落在对角线AC上的F点,
∴AF=AD=6,DE=EF,
∴CF=4,CE=8-EF,
∵EF2+CF2=CE2,即EF2+42=(8-EF)2,
∴EF=3,
∴DE=EF=3;
(2)∵将△ADE沿AE折叠,点D刚好落在对角线AC上的F点,
∴AF=AD,∠AFE=∠D=90°,
∴EF⊥AC,
∵AE=CE,
∴AF=CF,
∴AF=CF=AD=BC,
∴AC=2BC.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后边相等.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
9.三角形按边分类可分为( )
| A. | 不等边三角形、等边三角形 | |
| B. | 等腰三角形、等边三角形 | |
| C. | 不等边三角形、等腰三角形、等边三角形 | |
| D. | 不等边三角形、等腰三角形 |
 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),与y轴的交点在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x=1.下列结论: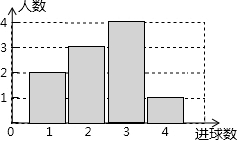 体育课上,老师为了解女学生定点投篮的情况,随机抽取10名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
体育课上,老师为了解女学生定点投篮的情况,随机抽取10名女生进行每人4次定点投篮的测试,进球数的统计如图所示.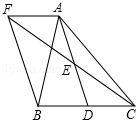 如图,点D是△ABC的边BC上一点,点E是AD的中点,过点A作AF∥BC,交CE的延长线于F,连接BF.
如图,点D是△ABC的边BC上一点,点E是AD的中点,过点A作AF∥BC,交CE的延长线于F,连接BF. 如图,在直角坐标系中,A、B的坐标分别为(4,0),(0,2),将线段AB向上平移m个单位得到A′B′,如果△OA′B′为等腰三角形,那么m的值为2或3或2$\sqrt{5}$-2.
如图,在直角坐标系中,A、B的坐标分别为(4,0),(0,2),将线段AB向上平移m个单位得到A′B′,如果△OA′B′为等腰三角形,那么m的值为2或3或2$\sqrt{5}$-2.