题目内容
14.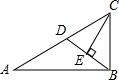 如图,在Rt△ABC中,AB=8,BC=6,BD是斜边AC上的中线,CE⊥DB,则CE=4.8.
如图,在Rt△ABC中,AB=8,BC=6,BD是斜边AC上的中线,CE⊥DB,则CE=4.8.
分析 由勾股定理得AC=10,由直角三角形斜边上的中线定理得到BD=5,S△BCD=$\frac{1}{2}$S△ABC=12,由三角形的面积公式即可求得结论.
解答 解:在Rt△ABC中,
∵AB=8,BC=6,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
∵BD是斜边AC上的中线,
∴BD=$\frac{1}{2}$×10=5,S△BCD=$\frac{1}{2}$S△ABC=$\frac{1}{2}×$$\frac{1}{2}$×8×6=12,
∴CE=$\frac{2{S}_{△BCD}}{BD}$=4.8,
故答案为4.8.
点评 本题主要考查了勾股定理,直角三角形斜边上的中线,三角形的面积公式,熟练掌握直角三角形斜边上的中线定理是解决问题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
5.把函数y=-2x的图象向下平移1个单位,所得图象的函数解析式为( )
| A. | y=-2x+1 | B. | y=-2x-1 | C. | y=-2(x-1) | D. | y=-2(x+1) |
19.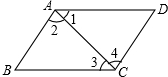 如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
 如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )
如图,在四边形ABCD中,要得到AB∥CD,只需要添加一个条件,这个条件可以是( )| A. | ∠1=∠3 | B. | ∠2=∠4 | C. | ∠B=∠D | D. | ∠1+∠2+∠B=180° |

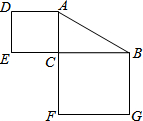 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为225.
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为225.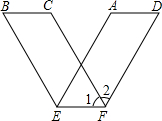 用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案,已知图中∠1=62°,则∠2的度数为56°.
用平行四边形纸条沿对边AB、CD上的点E、F所在的直线折成V字形图案,已知图中∠1=62°,则∠2的度数为56°.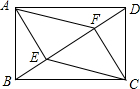 如图,在矩形ABCD中,E、F是对角线BD上的两点,且BE=DF,则四边形AECF是平行四边形图形.
如图,在矩形ABCD中,E、F是对角线BD上的两点,且BE=DF,则四边形AECF是平行四边形图形.
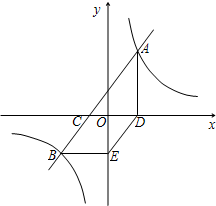 如图,已知直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.
如图,已知直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点.AD⊥x轴于点D,BE∥x轴且与y轴交于点E.