题目内容
17.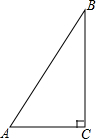 如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,求△ABC的周长和tanA的值.
如图,在△ABC中,∠C=90°,sinA=$\frac{4}{5}$,AB=10,求△ABC的周长和tanA的值.
分析 根据题中所给的条件,在直角三角形中解题,根据角的余弦值与三角形边的关系及勾股定理,可求出各边的长,代入三角函数进行求解.
解答 解:在Rt△ABC中,∠C=90°,AB=10
sinA=$\frac{BC}{AB}$=$\frac{4}{5}$,
∴BC=8,
AC=$\sqrt{A{B}^{2}-B{C}^{2}}=8$,
∴△ABC的周长=AB+AC+BC=24,
tanA=$\frac{BC}{AC}$=$\frac{4}{3}$.
点评 本题考查了利用锐角三角函数和勾股定理解直角三角形的能力,还考查解直角三角形的定义,由直角三角形已知元素求未知元素的过程,还考查了直角三角形的性质.

练习册系列答案
相关题目
7.一艘轮船在甲、乙两地之间航行,已知水流速度是5千米/小时,顺水航行需要6小时,逆水航行需要8小时,则甲乙两地间的距离是( )
| A. | 220千米 | B. | 240千米 | C. | 260千米 | D. | 350千米 |

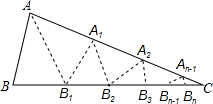 如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.
如图,△ABC中,沿∠BAC的平分线AB.折叠,剪掉重叠部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重叠部分,…;将余下部分沿∠An-1Bn-1折叠,经过n次折叠,若点Bn-1于点C重合,就称∠ABC的n阶“完美”角.