题目内容
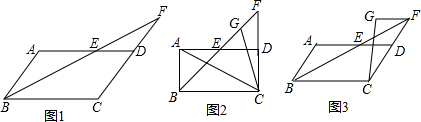
4.如图1,在?ABCD中,∠ABC的平分线BF交AD于点E,交CD的延长线于点F.(1)判断DE和DF的数量关系,并证明结论;
探究发现:
(2)如图2,若∠ABC=90°,G是EF的中点,求∠ACG的度数;
(3)如图3,若∠ABC=60°,FG∥DE,FG=DE,分别连接AC,CG.求∠ACG的度数.
分析 (1)由BF平分∠ABC,得到∠ABF=∠FBC,根据平行线的性质得到∠FED=∠FBC,∠F=∠ABF,等量代换得到∠FED=∠F,根据等腰三角形的判定即可得到结论;
(2)如图2,根据已知条件得到四边形ABCD是矩形,由BF平分∠ABC,得到∠ABF=∠FBC=45°,推出△EDF是等腰直角三角形,证得△AEG≌△CDG,根据全等三角形的性质得到AG=CG,推出△AGC是等腰直角三角形,根据等腰直角三角形的性质即可得到结论;
(3)如图3,延长BA,FG交于H,连接HC,得到四边形AHFD是平行四边形,证得△CBF是等腰三角形,根据等腰三角形的性质得到BC=CF,于是得到平行四边形BCFH是菱形,通过△AHC≌△GFC,得到∠ACH=∠GCF,即可得到结论.
解答 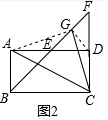 解:(1)DE=DF,
解:(1)DE=DF,
理由:∵BF平分∠ABC,
∴∠ABF=∠FBC,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠FED=∠FBC,∠F=∠ABF,
∴∠FED=∠F,
∴DE=DF;
(2)证明:如图2,连接AG,DG,
∵四边形ABCD是平行四边形,∠ABC=90°,
∴四边形ABCD是矩形,
∵BF平分∠ABC,
∴∠ABF=∠FBC=45°,
∵∠ADC=90°,CF∥AB,
∴∠F=45°,∠EDF=90°,
∴△EDF是等腰直角三角形,
∵G为EF的中点,
∴EG=DG=FG,DG⊥EF,
∵△ABE是等腰直角三角形,AB=DC
,∴AE=DC,∵∠DEF=∠GDF=45°,
∴∠AEG=∠CDG=135°,
在△AEG与△CDG中,$\left\{\begin{array}{l}{EG=DG}\\{∠AEG=∠CDG}\\{AE=CD}\end{array}\right.$,
∴△AEG≌△CDG,
∴AG=CG,
∵DG⊥EF,
∴∠DGC-∠CGB=90°,
∵∠DGC=∠EGA,
∴∠EGA+∠CGB=90°,
∴△AGC是等腰直角三角形,
∴∠ACG=45°;
(3)解:如图3,延长BA,FG交于H,连接HC,
∵AD∥GF,AB∥DF,
∴四边形AHFD是平行四边形,
∴DF=AH,
∵∠ABC=60°,BF平分∠ABC,
∴∠CBF=30°,∠BCD=120°,
∴∠CFB=30°,
∴△CBF是等腰三角形,
∴BC=CF,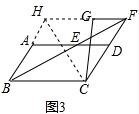
∴平行四边形BCFH是菱形,
∵∠ABC=60°,
∴△BCH,△CHF全等的等边三角形,
∴CH=CF,∠CHA=∠CFG=60°,
∵DE=AH,FG=DE,DF=AH,
∴AH=GF,
在△AHC与△GFC中,$\left\{\begin{array}{l}{CH=CF}\\{∠CHA=∠CFG}\\{AH=GF}\end{array}\right.$,
∴△AHC≌△GFC,
∴∠ACH=∠GCF,
∴∠ACG=∠ACH+∠HCG=∠GCF+∠HCG=∠HCF=60°.
点评 本题考查了全等三角形的判定和性质,平行四边形的判定和性质,菱形的判定和性质,等腰直角三角形的判定和性质,等边三角形的判定和性质,证得四边形AHFD是平行四边形是解题的关键.

| A. | 2.04×104 | B. | 2.04×105 | C. | 2.04×106 | D. | 20.4×104 |
| A. | 4 | B. | 2+$\sqrt{13}$ | C. | 5 | D. | 4+$\sqrt{13}$ |
 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3)、B(-3,1)、C(-1,3).请按下列要求画图:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-4,3)、B(-3,1)、C(-1,3).请按下列要求画图: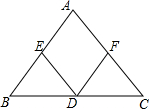 填写推理理由.
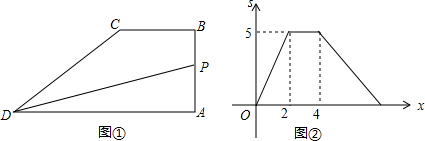
填写推理理由.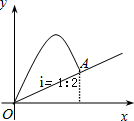 如图,小亮从斜坡的点O处抛出一个沙包,沙包轨迹抛物线的解析式为y=12x-x2,斜坡OA的坡度i=1:2,则沙包在斜坡的落点A的垂直高度是$\frac{23}{4}$.
如图,小亮从斜坡的点O处抛出一个沙包,沙包轨迹抛物线的解析式为y=12x-x2,斜坡OA的坡度i=1:2,则沙包在斜坡的落点A的垂直高度是$\frac{23}{4}$.