题目内容
16.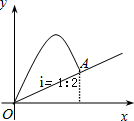 如图,小亮从斜坡的点O处抛出一个沙包,沙包轨迹抛物线的解析式为y=12x-x2,斜坡OA的坡度i=1:2,则沙包在斜坡的落点A的垂直高度是$\frac{23}{4}$.
如图,小亮从斜坡的点O处抛出一个沙包,沙包轨迹抛物线的解析式为y=12x-x2,斜坡OA的坡度i=1:2,则沙包在斜坡的落点A的垂直高度是$\frac{23}{4}$.
分析 设A点的坐标为(m,n),根据斜坡OA的坡度i=1:2,可得出m,n之间的关系,结合点在二次函数图象上即可列出关于m,n的二元二次方程组,解方程组求出n值即可.
解答 解:设A点的坐标为(m,n),
根据题意,得$\left\{\begin{array}{l}{n=12m-{m}^{2}}\\{\frac{n}{m}=\frac{1}{2}}\end{array}\right.$,
解得:n=0(舍去),或n=$\frac{23}{4}$,
故答案为:$\frac{23}{4}$.
点评 本题考查了二次函数的应用、坡度角问题以及解二元二次方程组,解题的关键是列出关于m、n的二元二次方程组.本题属于中档题,难度不大,但涉及到的知识点较多,解题的关键是结合各知识点列出方程组.

练习册系列答案
相关题目
6.已知△ABC的三个内角∠A,∠B,∠C满足∠A=∠B=∠C,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 等边三角形 | D. | 钝角三角形 |
8.2016年2月19日,经国务院批准,设立无锡市新吴区,将无锡市原新区的鸿山、旺庄、硕放、梅村、新安街道划和滨湖区的江溪街道归新吴区管辖.新吴区现有总人口322819人,这个数据用科学记数法(精确到千位)可表示为( )
| A. | 323×103 | B. | 3.22×105 | C. | 3.23×105 | D. | 0.323×106 |
11.下列计算正确的是( )
| A. | $\sqrt{(-5)^{2}}=-5$ | B. | -($\sqrt{5}$)2=5 | C. | $\sqrt{25-4}=5-2$ | D. | -$\sqrt{\frac{5}{4}}=-\frac{\sqrt{5}}{2}$ |
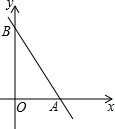 如图,在平面直角坐标系xOy中,直线AB过点A(3,0)、B(0,m)(m>0),tan∠BAO=2.
如图,在平面直角坐标系xOy中,直线AB过点A(3,0)、B(0,m)(m>0),tan∠BAO=2.