题目内容
如图，已知：某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆影长时，因旗杆靠近一幢房子，影子不全落在地面上，有一部分落在墙上，他测得落在地面上的影长为9米，留在墙上的影长CD为2米，求旗杆的高度．考点：相似三角形的应用
专题：
分析：旗杆的高度=AE+EB所对应的物长，把相关数值代入即可求解．
解答：
解：过D作DE⊥AB于E，
∵CD⊥BC，AB⊥BC，
∴∠EBC=∠DCB=∠AED=90°
∴四边形CDBE为矩形，
BC=DE=9，CD=BE=2
设AE=xm．
则1：1.5=x：9，
解得：x=6．
故旗杆高AB=AE+BE=6+2=8米．
解：过D作DE⊥AB于E，∵CD⊥BC，AB⊥BC，
∴∠EBC=∠DCB=∠AED=90°
∴四边形CDBE为矩形，
BC=DE=9，CD=BE=2
设AE=xm．
则1：1.5=x：9，
解得：x=6．
故旗杆高AB=AE+BE=6+2=8米．
点评：本题考查了相似三角形的应用，解决本题的难点在于得到旗杆高度的组成部分．
练习册系列答案
相关题目
将图甲中阴影部分的小长方形变换到图乙位置，你能根据两个图形的面积关系得到的数学公式是（ ）
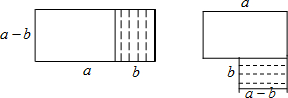
| A、（a+b）（a-b）=a2-b2 |
| B、（a+b）2=a2+2ab+b2 |
| C、（a-b）2=a2-2ab+b2 |
| D、a2-ab=a（a-b） |
如图，已知正方形OABC的面积是9，点O为坐标原点，点B是反比例函数y=