题目内容
 如图所示,CZ=
如图所示,CZ=| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
考点:三角形的面积
专题:
分析:连接CX,AY,BZ,设△XYZ的面积是2a,根据CZ=
YZ,AX=
XZ,BY=
XY分别求出△CXZ、△AYX、△BYZ的面积,再求出△ABY、△BCZ和△ACX的面积,求出三角形ABC的面积,即可得出答案.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
解答: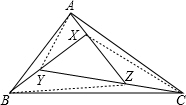 解:连接CX,AY,BZ,
解:连接CX,AY,BZ,
设△XYZ的面积是2a,
∵CZ=
YZ,AX=
XZ,BY=
XY,
∴△CXZ的面积是
×2a=a,△AYX的面积是
×2a=a,△BYZ的面积
×2a=a,
∵CZ=
YZ,AX=
XZ,BY=
XY,
∴△ABY的面积是
×a=
a,
同理△BCZ和△ACX的面积都是
a,
∴△ABC的面积是:2a+a+a+a+
a+
a+
a=
a,
∴△ABC与△XYZ的面积之比是2a:(
a)=4:13.
 解:连接CX,AY,BZ,
解:连接CX,AY,BZ,设△XYZ的面积是2a,
∵CZ=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
∴△CXZ的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵CZ=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
∴△ABY的面积是
| 1 |
| 2 |
| 1 |
| 2 |
同理△BCZ和△ACX的面积都是
| 1 |
| 2 |
∴△ABC的面积是:2a+a+a+a+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 13 |
| 2 |
∴△ABC与△XYZ的面积之比是2a:(
| 13 |
| 2 |
点评:本题考查了三角形的面积的应用,注意:等高的三角形的面积比等于对应的边之比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将图甲中阴影部分的小长方形变换到图乙位置,你能根据两个图形的面积关系得到的数学公式是( )
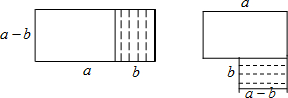

| A、(a+b)(a-b)=a2-b2 |
| B、(a+b)2=a2+2ab+b2 |
| C、(a-b)2=a2-2ab+b2 |
| D、a2-ab=a(a-b) |
 如图,已知正方形OABC的面积是9,点O为坐标原点,点B是反比例函数y=
如图,已知正方形OABC的面积是9,点O为坐标原点,点B是反比例函数y= 如图,在△ABC中,∠BAC=90°,点G是△ABC的重心,DE过点G,且DE∥BC,BC=8,求DE的长.
如图,在△ABC中,∠BAC=90°,点G是△ABC的重心,DE过点G,且DE∥BC,BC=8,求DE的长. 如图,连接网格中的AB,BC,AC,写出相等的边、相等的角(不能添加字母)并画出△ABC的对称轴.
如图,连接网格中的AB,BC,AC,写出相等的边、相等的角(不能添加字母)并画出△ABC的对称轴.