题目内容
 如图,已知AB、AC是⊙O的弦,AD平分∠BAC交⊙O于D,弦DE∥AB交AC于P,求证:OP平分∠APD.
如图,已知AB、AC是⊙O的弦,AD平分∠BAC交⊙O于D,弦DE∥AB交AC于P,求证:OP平分∠APD.考点:圆的认识,平行线的性质,全等三角形的判定与性质
专题:证明题
分析:作OM⊥AC于M,ON⊥DE于N,如图,由∠BAD=∠CAD,根据圆周角定理得CD弧=BD弧,由DE∥AB得∠ADE=∠BAD,得到AE弧=BD弧,所以AE弧=CD弧,则AC弧=ED弧,根据圆心角、弦、弧的关系得到AC=DE,然后根据在同圆或等圆中,相等的弦所对应的弦心距相等得到OM=ON,再根据角平分线定理的逆定理可判断
OP平分∠APD.
OP平分∠APD.
解答:证明 :作OM⊥AC于M,ON⊥DE于N,如图,
:作OM⊥AC于M,ON⊥DE于N,如图,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵CD弧=BD弧,
∵DE∥AB,
∴∠ADE=∠BAD,
∴AE弧=BD弧,
∴AE弧=CD弧,
∴AE弧+EC弧=EC弧+CD弧,即AC弧=ED弧,
∴AC=DE,
∴OM=ON,
∴OP平分∠APD.
 :作OM⊥AC于M,ON⊥DE于N,如图,
:作OM⊥AC于M,ON⊥DE于N,如图,∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵CD弧=BD弧,
∵DE∥AB,
∴∠ADE=∠BAD,
∴AE弧=BD弧,
∴AE弧=CD弧,
∴AE弧+EC弧=EC弧+CD弧,即AC弧=ED弧,
∴AC=DE,
∴OM=ON,
∴OP平分∠APD.
点评:本题考查了圆的认识:掌握与圆有关的概念(弦、直径、半径、弧、半圆、优弧、劣弧、等圆、等弧等).可以利用角平分线定理的逆定理证明角的平分线.

练习册系列答案
相关题目
计算(x4)3•x7的结果为( )
| A、x12 |
| B、x14 |
| C、x19 |
| D、x84 |
将图甲中阴影部分的小长方形变换到图乙位置,你能根据两个图形的面积关系得到的数学公式是( )
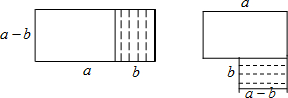

| A、(a+b)(a-b)=a2-b2 |
| B、(a+b)2=a2+2ab+b2 |
| C、(a-b)2=a2-2ab+b2 |
| D、a2-ab=a(a-b) |
 如图是函数y=-
如图是函数y=-