题目内容
1．
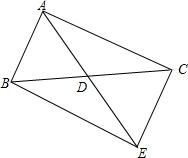如图，在△ABC中，AD为BC边上的中线，延长AD至E，使DE=AD，连接BE，CE（1）试判断四边形ABEC的形状；
（2）当△ABC满足什么条件时四边形ABEC是矩形？
分析 （1）得到四边形ABEC的对角线互相平分即可判定平行四边形；
（2）证得平行四边形的对角线相等即可证得矩形．
解答 解：（1）四边形ABEC是平行四边形；
证明：∵AD为BC边上的中线，
∴BD=CD，
∵AD=DE，
∴四边形ABEC的对角线互相平分，
∴四边形ABEC是平行四边形；
（2）当AD=BD时，四边形ABEC是矩形；
证明：∵AD=DE，BD=CD，AD=BD，
∴AE=BC，
∴四边形ABEC是矩形．
点评 本题考查了平行四边形的判定及矩形的判定，解题的关键是能够了解两种四边形的判定定理，难度不大．
练习册系列答案
相关题目
11．任意抛掷一枚均匀的骰子，结果朝上一面的点数为偶数的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |
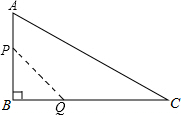如图，在△ABC中，∠B=90°，AB=12mm，BC=24mm，动点P从点A开始沿边AB向B以2mm/s的速度移动（不与点B重合），动点Q从点B开始沿边BC向C以4mm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，设运动的时间为x s，四边形APQC的面积为y mm2．
如图，∠B=∠C，D在BC上，∠BAD=30°，在AC上取AE=AD，∠ADE=∠AED，求∠EDC的度数．