题目内容
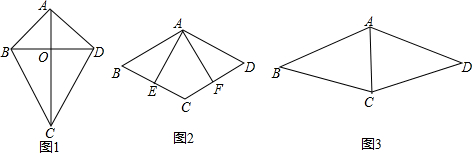
7.阅读下列材料:如图(1),在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为筝形.(1)写出筝形的两个性质(定义除外).
①∠BAC=∠DAC;②∠ABC=∠ADC.
(2)如图(2),在平行四边形ABCD中,点E、F分别在BC、CD上,且AE=AF,∠AEC=∠AFC.求证:四边形AECF是筝形.
(3)如图(3),在筝形ABCD中,AB=AD=26,BC=DC=25,AC=17,求筝形ABCD的面积.
分析 (1)在△ABC和△ADC中,△ABC≌△ADC即可,
(2)先判断出∠AEB=∠AFD在得到△AEB≌△AFD(AAS)然后判断出平行四边形ABCD是菱形即可;
(3)先判断出△ABC≌△ADC.得到S△ABC=S△ADC.利用勾股定理BH2=AB2-AH2=262-AH2.,BH2=CB2-CH2=252-(17-AH)2.即可.
解答 解:(1)在△ABC和△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{BC=DC}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC
∴∠BAC=∠DAC,∠ABC=∠ADC,
故答案为∠BAC=∠DAC,∠ABC=∠ADC
(2)证明:∵四边形ABCD是平行四边形,
∴∠B=∠D.
∵∠AEC=∠AFC,∠AEC+∠AEB=∠AFC+∠AFD=180°,
∴∠AEB=∠AFD.
∵AE=AF,
∴△AEB≌△AFD(AAS).
∴AB=AD,BE=DF.
∴平行四边形ABCD是菱形.
∴BC=DC,
∴EC=FC,
∴四边形AECF是筝形.
(3)如图
∵AB=AD,BC=DC,AC=AC,
∴△ABC≌△ADC.
∴S△ABC=S△ADC.
过点B作BH⊥AC,垂足为H.
在Rt△ABH中,BH2=AB2-AH2=262-AH2.
在Rt△CBH中,BH2=CB2-CH2=252-(17-AH)2.
∴262-AH2=252-(17-AH)2,
∴AH=10.
∴BH=24.
∴S△ABC=$\frac{1}{2}$×17×24=204.
∴筝形ABCD的面积为408.
点评 此题是四边形综合题,主要考查了菱形的性质和判定,三角形的全等的判定和性质,勾股定理,平行四边形的性质,解本题的关键是理解筝形的定义.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案| A. | a+a2=a3 | B. | a2•a3=a6 | C. | (2a2)3=2a6 | D. | a3÷a=a2 |
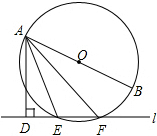 如图,已知直线l与⊙O相交于点E、F,AB是⊙O的直径,AD⊥l于点D,若∠DAE=22°,则∠BAF的大小为( )
如图,已知直线l与⊙O相交于点E、F,AB是⊙O的直径,AD⊥l于点D,若∠DAE=22°,则∠BAF的大小为( )| A. | 12° | B. | 18° | C. | 22° | D. | 30° |
| A. | $\sqrt{9}$=±3 | B. | (-a3)2=a6 | C. | a6÷a3=a2 | D. | (x+y)2=x2+y2 |
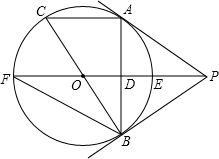 如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交与点C,连接AC,BF.
如图,PA为⊙O的切线,A为切点,直线PO交⊙O于点E,F过点A作PO的垂线AB垂足为D,交⊙O于点B,延长BO与⊙O交与点C,连接AC,BF.