题目内容
16．
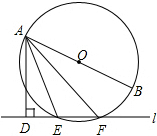如图，已知直线l与⊙O相交于点E、F，AB是⊙O的直径，AD⊥l于点D，若∠DAE=22°，则∠BAF的大小为（ ）| A． | 12° | B． | 18° | C． | 22° | D． | 30° |
分析 连接BE，根据圆周角定理可知∠AEB=90°，再由直角三角形两锐角互余得出∠AED的度数，根据余角的定义即可得出结论．
解答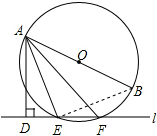 
解：连接BE，
∵AB是⊙O的直径，
∴∠AEB=90°．
∵AD⊥l于点D，∠DAE=22°，
∴∠AED=90°-22°=68°，
∴∠BEF=90°-∠AED=90°-68°=22°，
∴∠BAF=∠BEF=22°．
故选C．
点评 本题考查的是圆周角定理，熟知直径所对的圆周角是直角是解答此题的关键．
练习册系列答案
相关题目
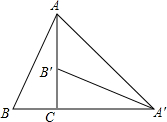如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连结AA′，若∠B=70°，则∠B′A′A的度数是25°．
如图，△ABC中，AB=AC=2，∠BAC=45°，将△ABC绕点A按顺时针方向旋转角α得到△AEF，且0°＜α≤180°，连接BE、CF相交于点D．
11．下列运算正确的是（ ）
| A． | x2•x=x2 | B． | 3x2-x2=2x2 | C． | （-3x）2=6x2 | D． | x8÷x4=x2 |