题目内容
15.如果一个自然数从高位和个位是由一个数字或几个数字重复出现组成,那么我们把这样的自然数叫循环数,被重复的一个或几个数字称为“循环节”,我们把“循环节”的数字个数叫做循环数的阶数,例如:252525,它由“25”依次重复出现组成,所以252525是循环数.它是2阶6位循环数;再如:11是1阶2位循环数:789789789是3阶9位循环数;345634563456是4阶12位循环数…(1)请你直接写出3个2阶6位循环数,猜想任意一个2阶6位循环数能否被7整除,并说明理由;
(2)已知一个能被13整除的2阶4位循环数,设循环节为xy,(0<x<5),求y与x之间的函数关系.
分析 (1)根据2阶6位循环数的定义,随便写出3个即可;结合数字的变化,找出变化规律“2阶6位循环数为任意的一个两位数×10101得出的”,根据10101是7的整数倍,即可得知任意一个2阶6位循环数能被7整除;
(2)结合(1)的规律可得出2阶4位循环数的变化规律“2阶4位循环数为任意的一个两位数×101得出的”,由101为质数可得出xy为13的倍数,结合x的取值范围即可得出y=3x.
解答 解:(1)依照2阶6位循环数的定义,随便写出3个2阶6位循环数:
131313;272727;868686.
任意一个2阶6位循环数能被7整除,理由如下:
结合数字的特点可得知:2阶6位循环数为任意的一个两位数×10101得出的.
∵10101÷7=1443,
∴任意一个2阶6位循环数能被7整除.
(2)结合(1)的规律可知:
2阶4位循环数为任意的一个两位数×101得出的.
∵101为质数,
∴xy为13的倍数,
又∵0<x<5,
∴y=3x.
当x=4时,y=3×4=12,4+1=5不符合题意,
∴0<x<4.
故y与x之间的函数关系为y=3x(0<x<4).
点评 本题考查了规律型中的数字的变化类,解题的关键是:(1)找出规律“2阶6位循环数为任意的一个两位数×10101得出的”;(2)找出规律“2阶4位循环数为任意的一个两位数×101得出的”.本题属于基础题,难度不大,解决该题型题目时,根据数字的特点找出变化规律是关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
3.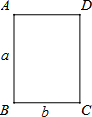 如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
 如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )
如图,矩形ABCD,AB=a,BC=b,a>b;以AB边为轴将矩形绕其旋转一周形成圆柱体甲,再以BC边为轴将矩形绕其旋转一周形成圆柱体乙;记两个圆柱体的体积分别为V甲、V乙,侧面积分别为S甲、S乙,则下列式子正确的是( )| A. | V甲>V乙 S甲=S乙 | B. | V甲<V乙 S甲=S乙 | ||
| C. | V甲=V乙 S甲=S乙 | D. | V甲>V乙 S甲<S乙 |
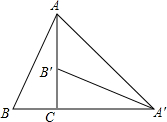 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连结AA′,若∠B=70°,则∠B′A′A的度数是25°.
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连结AA′,若∠B=70°,则∠B′A′A的度数是25°.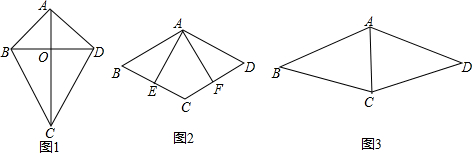
 如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.
如图,△ABC中,AB=AC=2,∠BAC=45°,将△ABC绕点A按顺时针方向旋转角α得到△AEF,且0°<α≤180°,连接BE、CF相交于点D.