题目内容
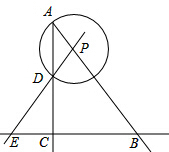 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.(1)求证:PE=PB;
(2)若AP=2,求CE的长;
(3)当以BE为直径的圆和⊙P外切时,求⊙P的半径.
考点:圆的综合题
专题:
分析:(1)利用等腰三角形的性质得出∠A=∠PDA,进而得出∠PBE=∠PEB,求出即可;
(2)由相似三角形的判定定理得出△ABC∽△DEC,在Rt△ABC中,根据勾股定理求出AB的长,再根据锐角三角函数的定义即可得出结论;
(3)设BE的中点为QM,连接PM,AP=x,根据等腰三角形三线合一的性质得出PM⊥BE,由切线的性质可得出PM=BM,由此可得出结论.
(2)由相似三角形的判定定理得出△ABC∽△DEC,在Rt△ABC中,根据勾股定理求出AB的长,再根据锐角三角函数的定义即可得出结论;
(3)设BE的中点为QM,连接PM,AP=x,根据等腰三角形三线合一的性质得出PM⊥BE,由切线的性质可得出PM=BM,由此可得出结论.
解答:(1)证明:∵PA=PD,
∴∠A=∠PDA,
∵∠EDC=∠PDA,∴∠A=∠EDC,
∵AC⊥BC,
∴∠PBE=∠PEB,
∴PB=PE;
(2)解:∵AP=DP,
∴∠PAD=∠PDA.
∴∠PAD=∠CDE.
∵∠ACB=∠DCE=90°,
∴△ABC∽△DEC.
∴∠ABC=∠DEC,
=
.
∴PB=PE.
Rt△ABC中,∠ABC=90°,
∵AC=4,BC=3,
∴AB=5.
∵AP=2,
∴PB=PE=3,DE=1,
∴
=
,
解得:CE=
;
(3)解:设M为BE的中点,则PM⊥BE,
若⊙P的半径为x,
则PB=5-x,PM=(5-x)sin∠ABC=
(5-x),
BM=(5-x)cos∠ABC=
(5-x),
∵⊙P与⊙M外切,
∴
(5-x)=
(5-x)+x
解得:x=
∴⊙P的半径为
.
∴∠A=∠PDA,
∵∠EDC=∠PDA,∴∠A=∠EDC,
∵AC⊥BC,
∴∠PBE=∠PEB,
∴PB=PE;
(2)解:∵AP=DP,
∴∠PAD=∠PDA.
∴∠PAD=∠CDE.
∵∠ACB=∠DCE=90°,
∴△ABC∽△DEC.

∴∠ABC=∠DEC,
| BC |
| EC |
| AB |
| DE |
∴PB=PE.
Rt△ABC中,∠ABC=90°,
∵AC=4,BC=3,
∴AB=5.
∵AP=2,
∴PB=PE=3,DE=1,
∴
| 3 |
| EC |
| 5 |
| 1 |
解得:CE=
| 3 |
| 5 |
(3)解:设M为BE的中点,则PM⊥BE,
若⊙P的半径为x,
则PB=5-x,PM=(5-x)sin∠ABC=
| 4 |
| 5 |
BM=(5-x)cos∠ABC=
| 3 |
| 5 |
∵⊙P与⊙M外切,
∴
| 4 |
| 5 |
| 3 |
| 5 |
解得:x=
| 5 |
| 6 |
∴⊙P的半径为
| 5 |
| 6 |
点评:本题考查的是圆的综合题,涉及到相似三角形的判定与性质、平行四边形的判定等知识,得出△ABC∽△DEC是解题关键.

练习册系列答案
相关题目

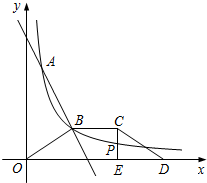 如图,一次函数y=ax+b与反比例函数y=
如图,一次函数y=ax+b与反比例函数y=