题目内容
以点P(n,n2+2n+1)(n≥1)为顶点的抛物线y=-x2+bx+c与x轴交于点A、B(点A在点B的左边).
(1)当n=1时,试求b和c的值;当n>1时,求b与n,c与n之间的关系式.
(2)若点P到AB的距离等于线段AB长的10倍,求此抛物线y=-x2+bx+c的解析式.
(3)设抛物线y=-x2+bx+c与y轴交于点D,O为原点,矩形OEFD的顶点E、F分别在x轴和该抛物线上,当矩形OEFD的面积为42时,求点P的坐标.
(1)当n=1时,试求b和c的值;当n>1时,求b与n,c与n之间的关系式.
(2)若点P到AB的距离等于线段AB长的10倍,求此抛物线y=-x2+bx+c的解析式.
(3)设抛物线y=-x2+bx+c与y轴交于点D,O为原点,矩形OEFD的顶点E、F分别在x轴和该抛物线上,当矩形OEFD的面积为42时,求点P的坐标.
考点:二次函数综合题
专题:
分析:(1)当n=1时,可求出P的坐标,由此可设抛物线的解析式为y=-(x-1)2+4,化为一般式左右对照即可求出b和c的值;当n>1时思路雷同;
(2)根据抛物线的解析式可求出A和B的坐标,又点P到x轴的距离为n2+2n+1,所以有n2+2n+1=10(2n+2),解方程求出n的值,进而可求出抛物线解析式;
(3)根据已知条件可求出OD,DF的长,再根据矩形的面积公式可得:OD•DF=2n(2n+1)=42,求出n的值,即可求出P的坐标.
(2)根据抛物线的解析式可求出A和B的坐标,又点P到x轴的距离为n2+2n+1,所以有n2+2n+1=10(2n+2),解方程求出n的值,进而可求出抛物线解析式;
(3)根据已知条件可求出OD,DF的长,再根据矩形的面积公式可得:OD•DF=2n(2n+1)=42,求出n的值,即可求出P的坐标.
解答:解:(1)当n=1时,点P坐标为(1,4),则y=-(x-1)2+4=-x2+2x+3=-x2+bx+c,
解得:b=2,c=3.
当n>1时,则y=-(x-n)2+n2+2n+1=-x2+2nx+2n+1=-x2+bx+c,
所以b=2n,c=2n+1.
(2)∵y=-(x-n)2+n2+2n+1=-x2+2nx+2n+1,
∴当y=0时,即-x2+2nx+2n+1=0.解得x1=-1,x2=2n+1.
由于点A在点B的左边,
∴A(-1,0)、B(2n+1,0),即AB=2n+1-(-1)=2n+2.
又∵点P到x轴的距离为n2+2n+1,
∴有n2+2n+1=10(2n+2).
解得n=19或n=-1(不合,舍去),
即n=19.
故,此时抛物线的解析式为y=-x2+38x+39.
(3)如图所示,
∵c=2n+1,
∴D(0,2n+1),
即OD=2n+1.又DF∥x轴,且D、F关于直线x=n对称,
∴F(2n,2n+1).有DF=2n.
从而OD•DF=2n(2n+1)=42,
解得n=3或n=-
(不合,舍去),即n=3.
故点P的坐标为(3,16).
解得:b=2,c=3.

当n>1时,则y=-(x-n)2+n2+2n+1=-x2+2nx+2n+1=-x2+bx+c,
所以b=2n,c=2n+1.
(2)∵y=-(x-n)2+n2+2n+1=-x2+2nx+2n+1,
∴当y=0时,即-x2+2nx+2n+1=0.解得x1=-1,x2=2n+1.
由于点A在点B的左边,
∴A(-1,0)、B(2n+1,0),即AB=2n+1-(-1)=2n+2.
又∵点P到x轴的距离为n2+2n+1,
∴有n2+2n+1=10(2n+2).
解得n=19或n=-1(不合,舍去),
即n=19.
故,此时抛物线的解析式为y=-x2+38x+39.
(3)如图所示,
∵c=2n+1,
∴D(0,2n+1),
即OD=2n+1.又DF∥x轴,且D、F关于直线x=n对称,
∴F(2n,2n+1).有DF=2n.
从而OD•DF=2n(2n+1)=42,
解得n=3或n=-
| 7 |
| 2 |
故点P的坐标为(3,16).
点评:本题着重考查了待定系数法求二次函数解析式、矩形的性质等知识点,综合性强,用到了数形结合的数学思想方法,其中第(3)中求出OD,OF的长解题是解题关键.

练习册系列答案
相关题目
 如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.
如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.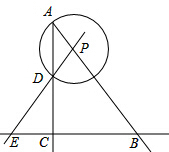 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,P是射线AB上的一个动点,以点P为圆心,PA为半径的⊙P与射线AC的另一个交点为D,直线PD交直线BC于点E.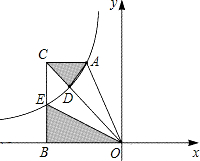 如图,在平面直角坐标系中,直角梯形AOBC的边OB在x轴的负半轴上,AC∥OB,∠OBC=90°,过A点的双曲线y=
如图,在平面直角坐标系中,直角梯形AOBC的边OB在x轴的负半轴上,AC∥OB,∠OBC=90°,过A点的双曲线y=