题目内容
20．
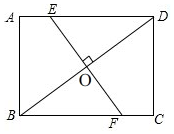如图，矩形ABCD中，已知AB=6，BC=8，BD的垂直平分线交AD于点E，交BC于点F，则BF的长为$\frac{25}{4}$．
分析 根据矩形的性质和勾股定理求出BD，证明△BOF∽△BCD，根据相似三角形的性质得到比例式，求出BF即可．
解答 解：∵四边形ABCD是矩形，
∴∠A=90°，又AB=6，AD=BC=8，
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=10，
∵EF是BD的垂直平分线，
∴OB=OD=5，∠BOF=90°，又∠C=90°，
∴△BOF∽△BCD，
∴$\frac{BO}{BC}$=$\frac{BF}{BD}$，即$\frac{5}{8}$=$\frac{BF}{10}$，
解得，BF=$\frac{25}{4}$，
故答案为：$\frac{25}{4}$．
点评 本题考查的是矩形的性质、线段垂直平分线的性质以及勾股定理的应用，掌握矩形的四个角是直角、对边相等以及线段垂直平分线的定义是解题的关键．
练习册系列答案
相关题目
10．
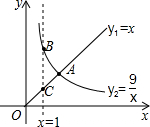函数y1=x（x≥0），y2=$\frac{9}{x}$（x＞0）的图象如图所示，则结论：
①两函数图象的交点A的坐标为（3，3 ）；
②当x＜3时，y2＞y1；
③当x=1时，BC=8；
④当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小．
其中正确结论的序号是（ ）
函数y1=x（x≥0），y2=$\frac{9}{x}$（x＞0）的图象如图所示，则结论：①两函数图象的交点A的坐标为（3，3 ）；
②当x＜3时，y2＞y1；
③当x=1时，BC=8；
④当x逐渐增大时，y1随着x的增大而增大，y2随着x的增大而减小．
其中正确结论的序号是（ ）
| A． | ①③④ | B． | ①②③④ | C． | ②③④ | D． | ①③ |
15．
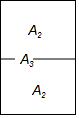复印纸的型号A0，A1，A2，A3、A4等，它们之间存在着这样一种关系：将其中某一型号（如A3）的复印纸较长边的中点对折后，就能得到两张下一型号（A4）的复印纸，且得到的两个矩形都和原来的矩形相似（如图），那么这些型号的复印纸的长宽之比为（ ）
复印纸的型号A0，A1，A2，A3、A4等，它们之间存在着这样一种关系：将其中某一型号（如A3）的复印纸较长边的中点对折后，就能得到两张下一型号（A4）的复印纸，且得到的两个矩形都和原来的矩形相似（如图），那么这些型号的复印纸的长宽之比为（ ）| A． | $\sqrt{2}$：1 | B． | $\sqrt{3}$：1 | C． | 1：$\sqrt{2}$ | D． | 3：1 |
将如图所示的长方形绕图中的虚线旋转360°得到的几何体是（ ）
同时抛掷两枚质地均匀的骰子，下列说法：（1）“两枚的点数都是3”的概率比“两枚的点数都是6”的概率大；（2）“两枚的点数相同”的概率是$\frac{1}{6}$；（3）“两枚的点数都是1”的概率最大；（4）“两枚的点数之和为奇数”与“两枚的点数之和为偶数”的概率相等．其中正确的是（ ）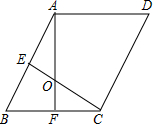
如图，在菱形ABCD中，∠B=60°，E、F分别是AB、BC的中点，AF、CE相交于点O，则∠AOC=120°．