题目内容
11．方程（x+5）（2x-7）=0可转化为两个一元一次方程为x+5=0或2x-7=0．分析 根据两因式的积为0，则这两个因式的值至少有一个为0可得．
解答 解：∵（x+5）（2x-7）=0，
∴x+5=0或2x-7=0，
故答案为：x+5=0、2x-7=0．
点评 本题主要考查因式分解法解一元二次方程，熟练掌握因式分解法解方程的概念是关键．
练习册系列答案
相关题目
2．用尺规作图，不能作出唯一直角三角形的是（ ）
| A． | 已知两条直角边 | |
| B． | 已知两个锐角 | |
| C． | 已知一直角边和直角边所对的一锐角 | |
| D． | 已知斜边和一直角边 |
16．下列各式中，属于分式的是（ ）
| A． | $\frac{3xy}{π}$ | B． | $\frac{5a-b}{2x-y}$ | C． | $\frac{{x}^{2}+1}{2}$ | D． | $\frac{x}{2}$-$\frac{1}{3}$ |
3．下列式子中，错误的是（ ）
| A． | $\sqrt{（-10）^{2}}$=10 | B． | （-2$\sqrt{2}$）2=8 | C． | （$\sqrt{-10}$）2=10 | D． | -$\sqrt{（-\frac{3}{5}）^{2}}$=-$\frac{3}{5}$ |
20．下列各式正确的是（ ）
| A． | $±\sqrt{0.36}$=±0.6 | B． | $\sqrt{9}=±3$ | C． | $\root{3}{（-3）^{3}}$=3 | D． | $\sqrt{（-2）^{2}}$=-2 |
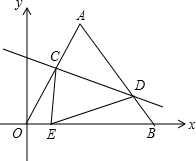如图坐标系中，O（0，0），A（6，6$\sqrt{3}$），B（12，0），将△OAB沿直线线CD折叠，使点A恰好落在线段OB上的点E处，若OE=$\frac{24}{5}$，则CE：DE的值是$\frac{7}{8}$．