题目内容
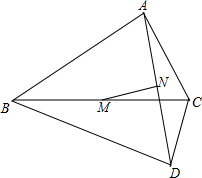
 已知,正方形ABCD的边长为10,AC、BD交于点O,点E是OB的中点,DG⊥CE于G,交OC于F,求EF的长.
已知,正方形ABCD的边长为10,AC、BD交于点O,点E是OB的中点,DG⊥CE于G,交OC于F,求EF的长.考点:正方形的性质,全等三角形的判定与性质
专题:
分析:由已知可得出△DCF≌△CBE,可得CF=BE,即可得出EF为中位线,易得出EF的长.
解答:解:∵在正方形ABCD中,DG⊥CE,
∴∠CDF=∠BCE,∠DCF=∠CBE=45°,
在△DCF和△CBE中,
,
∴△DCF≌△CBE(ASA)
∴CF=BE,
∵E是OB的中点,
∴F是OC的中点,
∴EF=
BC=5cm.
∴∠CDF=∠BCE,∠DCF=∠CBE=45°,
在△DCF和△CBE中,
|
∴△DCF≌△CBE(ASA)
∴CF=BE,
∵E是OB的中点,
∴F是OC的中点,
∴EF=
| 1 |
| 2 |
点评:本题主要考查了正方形的性质及全等三角形的判定与性质,解题的关键是得出△DCF≌△CBE.

练习册系列答案
相关题目
若实数a的平方根等于它本身,则a的取值为( )
| A、±1或0 | B、1或0 |
| C、0 | D、非负数 |
 如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )
如图,AB=AC,添加下列条件,能用SAS判断△ABE≌△ACD的是( )| A、∠B=∠C |
| B、∠AEB=∠ADC |
| C、AE=AD |
| D、BE=DC |
 如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,AB=3
如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,AB=3