题目内容
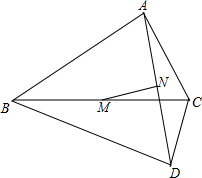 如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,AB=3
如图,在Rt△ABC中,∠BAC=90°,∠ABC=30°,AB=3| 5 |
| 3 |
考点:勾股定理,直角三角形斜边上的中线
专题:
分析:连AM,因∠BAC=90°,∠BDC=90°,故A,D,B,C四点共圆,M为圆心,BC为直径,又因NAD的中点,故MN⊥平分AD,AN=
2AD=
,又因∠ABC=30度,AB=3
,故BC=2
,即AM=
BC=
,所以利用勾股定理可得MN2=AM2-AN2=15-3=12,即MN=2
,问题得解.
| 1 |
| 2 |
| 3 |
| 5 |
| 15 |
| 1 |
| 2 |
| 15 |
| 3 |
解答:解:连AM,
∵∠BAC=90°,∠BDC=90°,
∴A,D,B,C四点共圆,M为圆心,BC为直径,
又∵NAD的中点,
∴MN⊥平分AD,AN=
2AD=
,
∵∠ABC=30°,AB=3
,
∴BC=2
,即AM=
BC=
,
∴MN2=AM2-AN2=15-3=12,
∴MN=2
.
∵∠BAC=90°,∠BDC=90°,

∴A,D,B,C四点共圆,M为圆心,BC为直径,
又∵NAD的中点,
∴MN⊥平分AD,AN=
| 1 |
| 2 |
| 3 |
∵∠ABC=30°,AB=3
| 5 |
∴BC=2
| 15 |
| 1 |
| 2 |
| 15 |
∴MN2=AM2-AN2=15-3=12,
∴MN=2
| 3 |
点评:本题考查了勾股定理的运用、直角三角形斜边上中线的性质以及圆周角定理的运用,题目的综合性较强,难度中等.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
下列函数中,属于反比例函数的是( )
A、y=
| ||
B、y=-
| ||
| C、y=2+3x | ||
| D、y=2+3x2 |
把分式
中的m和n都扩大为原来的2倍,那么分式的值( )
| mn |
| m-n |
| A、扩大为原来的2倍 |
| B、扩大为原来的4倍 |
| C、不变 |
| D、缩小为原来的2倍 |
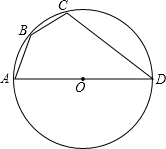 已知:四边形ABCD内接于以AD为直径的⊙O,且AD=4,AB=CB=1,求:CD的长.
已知:四边形ABCD内接于以AD为直径的⊙O,且AD=4,AB=CB=1,求:CD的长. 已知,正方形ABCD的边长为10,AC、BD交于点O,点E是OB的中点,DG⊥CE于G,交OC于F,求EF的长.
已知,正方形ABCD的边长为10,AC、BD交于点O,点E是OB的中点,DG⊥CE于G,交OC于F,求EF的长.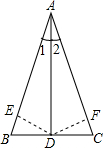 已知在△ABC中,D是BC的中点,∠1=∠2,求证:AB=AC.
已知在△ABC中,D是BC的中点,∠1=∠2,求证:AB=AC. 如图所示,在平行四边形ABCD中,对角线AC平分∠DAB.这个四边形是菱形吗?简述你的理由.
如图所示,在平行四边形ABCD中,对角线AC平分∠DAB.这个四边形是菱形吗?简述你的理由.