题目内容
△ABC中,∠C=90°,G为其重心,若CG=2,那么AB= .
考点:三角形的重心
专题:
分析:如图,运用三角形重心的性质,求出DG=1,CD=3;运用直角三角形斜边上的中线等于斜边的一半,即可解决问题.
解答: 解:如图,∵点G为△ABC的重心,且CG=2,
解:如图,∵点G为△ABC的重心,且CG=2,
∴CG=2DG=2,
∴DG=1,CD=3;
由直角三角形的性质得:AB=2CD=6,
故答案为6.
 解:如图,∵点G为△ABC的重心,且CG=2,
解:如图,∵点G为△ABC的重心,且CG=2,∴CG=2DG=2,
∴DG=1,CD=3;
由直角三角形的性质得:AB=2CD=6,
故答案为6.
点评:该题主要考查了三角形重心的性质及其应用问题;解题的关键是牢固掌握三角形重心的性质,这是灵活运用、解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,是一个正方体的展开图,正方体的每个面都有一个数字,只有一对相对两面的数字的积是有理数,这个有理数是( )
如图,是一个正方体的展开图,正方体的每个面都有一个数字,只有一对相对两面的数字的积是有理数,这个有理数是( )| A、4 | B、6 | C、9 | D、10 |
将二次函数y=x2的图象向下平移1个单位,再向右平移1个单位后所得图象的函数表达式为( )
| A、y=(x+1)2+1 |
| B、y=(x+1)2-1 |
| C、y=(x-1)2+1 |
| D、y=(x-1)2-1 |
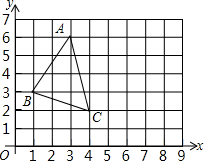 如图,△ABC的顶点坐标分别为A(3,6),B(1,3),C(4,2),将△ABC绕点C顺时针旋转90°,得到△A′B′C.
如图,△ABC的顶点坐标分别为A(3,6),B(1,3),C(4,2),将△ABC绕点C顺时针旋转90°,得到△A′B′C.

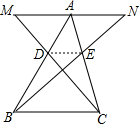 如图,MN经过△ABC的顶点A,MN∥BC,AM=AN,MC交AB于E.
如图,MN经过△ABC的顶点A,MN∥BC,AM=AN,MC交AB于E. 如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,如果AC=
如图,在Rt△ABC中,∠C=90°,点G是△ABC的重心,如果AC=