题目内容
1.①计算:cot44°•cot45°•cot46°=1②一般地,当α为锐角时sin(180°+α)=-sinα,如sin210°=sin(180°+30°)=-sin30°=$\frac{1}{2}$,由此可知:sin240°的值为-$\frac{\sqrt{3}}{2}$.
分析 ①根据特殊角三角函数值,可得实数的运算,根据实数的运算,可得答案;
②当α为锐角时sin(180°+α)=-sinα,可得特殊角三角函数,根据特殊角三角函数值,可得答案.
解答 解:①cot44°•cot45°•cot46°
=tan46°•cot45°•cot46°
=cot45°
=1;
②sin240°=sin(180°+60°)
=-sin60°
=-$\frac{{\sqrt{3}}}{2}$,
故答案为:1,-$\frac{\sqrt{3}}{2}$.
点评 本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
12.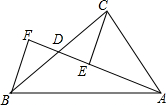 如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
①△BDF≌△CDE;②CE=BF;③ABD和△ACD的面积相等;④BF∥CE.
 如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )①△BDF≌△CDE;②CE=BF;③ABD和△ACD的面积相等;④BF∥CE.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10. 已知:正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,则( )
已知:正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,则( )
 已知:正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,则( )
已知:正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,则( )| A. | k1=$\frac{1}{4}$,k2=4 | B. | k1=4,k2=$\frac{1}{4}$ | C. | k1=$\frac{1}{4}$,k2=-4 | D. | k1=-$\frac{1}{4}$,k2=4 |

 在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图,
在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图, 如图,是一个包装盒的三视图,则这个包装盒的表面积是600πcm2(结果保留π)
如图,是一个包装盒的三视图,则这个包装盒的表面积是600πcm2(结果保留π) 如图,已知数轴上点A表示的数为a,点B表示的数为b,且满足(a-6)2+|b+4|=0.
如图,已知数轴上点A表示的数为a,点B表示的数为b,且满足(a-6)2+|b+4|=0.