题目内容
10. 已知:正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,则( )
已知:正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点M(a,1),MN⊥x轴于点N(如图),若△OMN的面积等于2,则( )| A. | k1=$\frac{1}{4}$,k2=4 | B. | k1=4,k2=$\frac{1}{4}$ | C. | k1=$\frac{1}{4}$,k2=-4 | D. | k1=-$\frac{1}{4}$,k2=4 |
分析 此题只要求出M点的坐标,就解决问题了,根据M点在正比例函数y=k1x的图象与反比例函数的图象上,根据△OMN的面积等于2,求出a值,从而求出M点坐标.
解答 解:∵MN⊥x轴,点M(a,1),
∴S△OMN=$\frac{1}{2}$a=2,
∴a=4,
∴M(4,1),
∵正比例函数y=k1x的图象与反比例函数y=$\frac{{k}_{2}}{x}$(x>0)的图象交于点M(4,1),
∴$\left\{\begin{array}{l}{1=4{k}_{1}}\\{1=\frac{{k}_{2}}{4}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=\frac{1}{4}}\\{{k}_{2}=4}\end{array}\right.$,
故选A.
点评 此题考查了正比例函数和反比例函数的交点问题,根据面积求得M点的坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F.连接DE,则DF的长是( )
如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F.连接DE,则DF的长是( )
 如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F.连接DE,则DF的长是( )
如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F.连接DE,则DF的长是( )| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\frac{7}{8}$ | D. | $\frac{25}{8}$ |




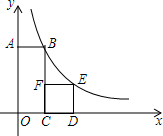 如图,点B、E在反比例函数y=$\frac{k}{x}$的图象上,矩形OABC的顶点A在y轴的正半轴上,正方形CDEF的顶点C、D在x轴的正半轴上,顶点F在BC上.若正方形CDEF的边长为2,且CB=3CF,则反比例函数的关系式为y=$\frac{6}{x}$.
如图,点B、E在反比例函数y=$\frac{k}{x}$的图象上,矩形OABC的顶点A在y轴的正半轴上,正方形CDEF的顶点C、D在x轴的正半轴上,顶点F在BC上.若正方形CDEF的边长为2,且CB=3CF,则反比例函数的关系式为y=$\frac{6}{x}$. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,请在图(1)中画出一个格点三角形,使它与图(1)中的△ABC相似.
下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,请在图(1)中画出一个格点三角形,使它与图(1)中的△ABC相似.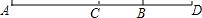 如图,C为线段AD上一点,B为CD的中点,AD=12cm,BD=3cm.
如图,C为线段AD上一点,B为CD的中点,AD=12cm,BD=3cm.