题目内容
14. 已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M,点F在线段ME上,且满足CF=AD,MF=MA.
已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M,点F在线段ME上,且满足CF=AD,MF=MA.(1)求证:△DME≌△CME;
(2)若∠MFC=120°,求∠BAM的度数;
(3)试猜想∠PMB与∠FCM有怎样的数量关系?请证明你的结论.
分析 (1)根据垂直平分线的性质得MD=MC,根据SSS即可证明,由可以用SAS进行证明.
(2)由△AMD≌△FMC得∠DAM=∠MFC=120°即可解决问题.
(3)结论:∠FCM=2∠PMB,由△AMD≌△FMC得∠ADM=∠FCM,由AD∥BC得∠ADM=∠DMC,再证明∠DME=∠CME即可.
解答 (1)证明:∵DE=EC,ME⊥CD,
∴MD=MC,
在△DME和△CME中,
$\left\{\begin{array}{l}{MD=MC}\\{ME=ME}\\{ED=EC}\end{array}\right.$,
∴△DME≌△CME.
(2)证明:在△AMD和△FMC中,
$\left\{\begin{array}{l}{AM=FM}\\{MD=MC}\\{AD=CF}\end{array}\right.$,
∴△AMD≌△FMC,
∴∠DAM=∠MFC=120°,
∵AD∥BC,∠ABC=90°,
∴∠DAB+∠ABC=180°,
∴∠DAB=90°,
∴∠MAB=∠MAD-∠DAB=30°.
(3)结论:∠FCM=2∠PMB.
理由:∵△AMD≌△FMC,
∴∠ADM=∠FCM,
∵AD∥BC,
∴∠ADM=∠DMC,
∴∠DMC=∠FCM,
∵MD=MC,ME⊥CD,
∴∠DME=∠CME,
∴∠FCM=2∠PMB.
点评 本题考查全等三角形的判定和性质、相等垂直平分线的性质、平行线的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列图形选自历届世博会会徽,其中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.下列交通标志中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
6.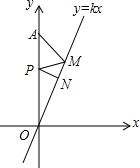 如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,4),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )
如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,4),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )
 如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,4),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )
如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,4),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )| A. | 2 | B. | 4sin40° | ||
| C. | 2$\sqrt{3}$ | D. | 4sin20°(1+cos20°+sin20°cos20°) |
 如图所示,等边△ABC中,D为BC边上一点,∠DAE=60°,AE交∠ACB的外角平分线于点E,△ADE是等边三角形吗?说明理由.
如图所示,等边△ABC中,D为BC边上一点,∠DAE=60°,AE交∠ACB的外角平分线于点E,△ADE是等边三角形吗?说明理由.