题目内容
8.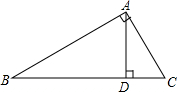 如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,则∠B=∠DAC,∠C=∠BAD.
如图所示,在△ABC中,∠BAC=90°,AD⊥BC于点D,则∠B=∠DAC,∠C=∠BAD.
分析 先根据直角三角形两锐角互余得出∠B+∠C=90°,再由三角形的高的定义得出∠ADB=∠ADC=90°,那么根据直角三角形两锐角互余得出∠DAC+∠C=90°,∠B+∠BAD=90°,然后根据同角的余角相等即可得到∠B=∠DAC,∠C=∠BAD.
解答 解:∵在△ABC中,∠BAC=90°,
∴∠B+∠C=90°,
∵AD⊥BC于点D,
∴∠ADB=∠ADC=90°,
∴∠DAC+∠C=90°,∠B+∠BAD=90°,
∴∠B=∠DAC,∠C=∠BAD.
故答案为DAC,BAD.
点评 本题考查了直角三角形的性质,余角的性质,三角形的高,掌握直角三角形中,两个锐角互余是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
18.若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则b,k的值分别( )
| A. | 0,5 | B. | -4,1 | C. | -4,5 | D. | -4,-1 |
16. 如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )
如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )
 如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )
如图,AB是圆O的直径,AB⊥CD于点E,若CD=8,则DE等于( )| A. | 3 | B. | 5 | C. | 4 | D. | 6 |
20.把一个正方形的一边增加2cm,另一边增加1cm,得到的矩形面积的2倍比正方形的面积多11cm2.设这个正方形的边长为x cm,依题意可得方程为( )
| A. | (x+2)(x+1)=2x2+14 | B. | 2(x+2)(x+1)=x2+11 | C. | 2(x-2)(x-1)=x2+11 | D. | (x-2)(x-1)=2x2+11 |
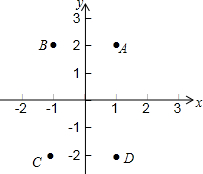 如图,平面内四个点的坐标分别为A(1,2),B(-1,2),C(-1,-2),D(1,-2),依次连接点A,B,C,D,则四边形ABCD的面积为( )
如图,平面内四个点的坐标分别为A(1,2),B(-1,2),C(-1,-2),D(1,-2),依次连接点A,B,C,D,则四边形ABCD的面积为( ) 如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,点B的坐标为(3,-$\frac{3}{2}$)直线l1,l2交于点C.
如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,点B的坐标为(3,-$\frac{3}{2}$)直线l1,l2交于点C. 在平面直角坐标系中,将坐标是(0,4),(1,0),(2,4),(3,0),(4,4)的点用线段依次连接起来形成一个图案.
在平面直角坐标系中,将坐标是(0,4),(1,0),(2,4),(3,0),(4,4)的点用线段依次连接起来形成一个图案.