题目内容
 在正方形ABCD中,O是对角线AC、BD的交点,分别过点A、B、C、D作BD、AC的平行线交于点E、F、G、H.
在正方形ABCD中,O是对角线AC、BD的交点,分别过点A、B、C、D作BD、AC的平行线交于点E、F、G、H.求证:四边形EFGH是正方形.
考点:正方形的判定与性质
专题:证明题
分析:依据“由两组对边相互平行的四边形为平行四边形”推知四边形EFGH是平行四边形,根据正方形的对角线互相垂直得到AC⊥BD,由平行线的性质推知EH⊥GH,即四边形EFGH是正方形.
解答:证明:∵四边形ABCD是正方形,
∴AC⊥BD.
又∵分别过点A、B、C、D作BD、AC的平行线,即EH∥FG∥BD,EH=FG=BD,EF∥HG∥AC,EF=HG=AC,
∴四边形EFGH是菱形,EH⊥GH,
∴四边形EFGH是正方形.
∴AC⊥BD.
又∵分别过点A、B、C、D作BD、AC的平行线,即EH∥FG∥BD,EH=FG=BD,EF∥HG∥AC,EF=HG=AC,
∴四边形EFGH是菱形,EH⊥GH,
∴四边形EFGH是正方形.
点评:本题考查了正方形的判定与性质.正方形的判定没有固定的方法,只要判定既是矩形又是菱形就可以判定.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
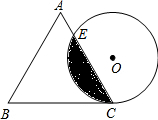 如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于E.
如图,边长为4cm的等边三角形ABC与⊙O等高(即高与直径相等),⊙O与BC相切于点C,⊙O与AC相交于E. 如图,由小正方形组成格点图形,已知格点A坐标为(-1,-2),则格点B的坐标为
如图,由小正方形组成格点图形,已知格点A坐标为(-1,-2),则格点B的坐标为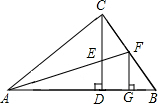 如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、BC于点E、F.且FG⊥AB,垂足为G,
如图,CD为Rt△ABC斜边上的高,∠BAC的平分线分别交CD、BC于点E、F.且FG⊥AB,垂足为G,