题目内容
2.已知函数y=(n+1)xm+mx+1-n(m,n为实数)(1)当m,n取何值时,此函数是我们学过的哪一类函数?它一定与x轴有交点吗?请判断并说明理由;
(2)若它是一个二次函数,假设n>-1,那么:
①当x<0时,y随x的增大而减小,请判断这个命题的真假并说明理由;
②它一定经过哪个点?请说明理由.
分析 认真审题,首先根据我们所学过的三类函数进行分析,并分类讨论,可得出第一题的答案,再根据二次函数的性质,进行分析可得出第二问的答案.
解答 解:(1)①当m=1,n≠-2时,函数y=(n+1)xm+mx+1-n(m,n为实数)是一次函数,它一定与x轴有一个交点,
∵当y=0时,(n+1)xm+mx+1-n=0,∴x=$\frac{1-n}{n+2}$,
∴函数y=(n+1)xm+mx+1-n(m,n为实数)与x轴有交点;
②当m=2,n≠-1时,函数y=(n+1)xm+mx+1-n(m,n为实数)是二次函数,
当y=0时,y=(n+1)xm+mx+1-n=0,
即:(n+1)x2+2x+1-n=0,
△=22-4(1+n)(1-n)=4n2≥0;
∴函数y=(n+1)xm+mx+1-n(m,n为实数)与x轴有交点;
③当n=-1,m≠0时,函数y=(n+1)xm+mx+1-n是一次函数,当y=0时,x=$\frac{n-1}{m}$,
∴函数y=(n+1)xm+mx+1-n(m,n为实数)与x轴有交点;
(2)①假命题,若它是一个二次函数,
则m=2,函数y=(n+1)x2+2x+1-n,
∵n>-1,∴n+1>0,
抛物线开口向上,
对称轴:-$\frac{b}{2a}$=$-\frac{2}{2(n+1)}$=-$\frac{1}{n+1}$<0,
∴对称轴在y轴左侧,当x<0时,y有可能随x的增大而增大,也可能随x的增大而减小,
②当x=1时,y=n+1+2+1-n=4.
当x=-1时,y=0.
∴它一定经过点(1,4)和(-1,0).
点评 本题主要考查了一次函数、二次函数、反比例函数的定义,以及二次函数的性质,是一道综合题目,在草纸上画出草图,根据数形结合的思想进行解答是解题的关键,注意总结.

| A. | a$\sqrt{b}$ | B. | -a$\sqrt{b}$ | C. | a$\sqrt{-b}$ | D. | -a$\sqrt{-b}$ |
| A. | ${9}^{\frac{1}{2}}$=±3 | B. | $\root{3}{-27}$=3 | C. | (-3)n=0 | D. | 3-2=$\frac{1}{9}$ |
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
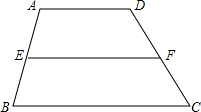 (1)叙述三角形中位线定理,并运用平行四边形的知识证明;
(1)叙述三角形中位线定理,并运用平行四边形的知识证明;