题目内容
3.小敏乘动车从甲地出发经过乙地前往丙地,图1是甲、乙、丙三地的位置示意图.动车匀速行驶,图2是动车离乙地路程y(千米)与行驶时间x(小时)时间的函数关系图象.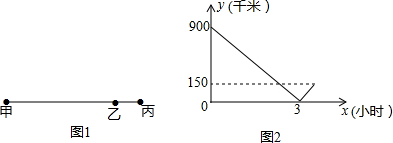
(1)填空:甲、丙两地距离为1050千米.
(2)求动车离乙地的路程y与行驶时间x之间的函数关系式,并写出x的取值范围.
分析 (1)根据函数图形可得,甲、丙两地距离为:900+150=1050(千米);
(2)分两种情况:当0≤x≤3时,设高速列车离乙地的路程y与行驶时间x之间的函数关系式为:y=kx+b,把(0,900),(3,0)代入得到方程组,即可解答;根据确定高速列车的速度为300(千米/小时),从而确定点A的坐标为(3.5,150),当3<x≤3.5时,设高速列车离乙地的路程y与行驶时间x之间的函数关系式为:y=k1x+b1,把(3,0),(3.5,150)代入得到方程组,即可解答.
解答 解:(1)根据函数图形可得,甲、丙两地距离为:900+150=1050(千米).
故答案为:1050.
(2)当0≤x≤3时,设高速列车离乙地的路程y与行驶时间x之间的函数关系式为:y=kx+b,
把(0,900),(3,0)代入得:$\left\{\begin{array}{l}{b=900}\\{3k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-300}\\{b=900}\end{array}\right.$,
∴y=-300x+900,
高速列车的速度为:900÷3=300(千米/小时),
150÷300=0.5(小时),3+0.5=3.5(小时)
如图2,点A的坐标为(3.5,150)
当3<x≤3.5时,设高速列车离乙地的路程y与行驶时间x之间的函数关系式为:y=k1x+b1,
把(3,0),(3.5,150)代入得:$\left\{\begin{array}{l}{3{k}_{1}+{b}_{1}=0}\\{3.5{k}_{1}+{b}_{1}=150}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=300}\\{{b}_{1}=-900}\end{array}\right.$,
∴y=300x-900,
∴y=$\left\{\begin{array}{l}{-300x+900(0≤x≤3)}\\{300x-900(3<x≤3.5)}\end{array}\right.$.
点评 本题考查了一次函数的应用,解决本题的关键是读懂图象,获取相关信息,用待定系数法求函数解析式.

| A. | 3a2-a2=2 | B. | a6•a3=a18 | C. | (a3)3=a6 | D. | x3÷x-1=x4 |
| A. | a2+a3=a5 | B. | 4a+2b=6ab | C. | ${(\frac{1}{{{a^2}+1}})^0}=1$ | D. | ${(2\sqrt{5})^2}=10$ |
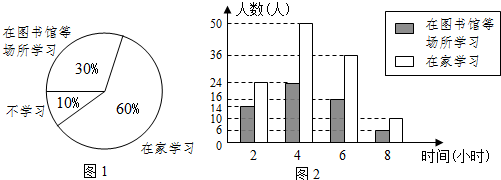
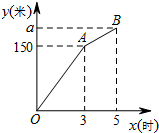 甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队又用了2小时完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y(米)与维修时间x(时)之间的函数图象如图所示.
甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队又用了2小时完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y(米)与维修时间x(时)之间的函数图象如图所示.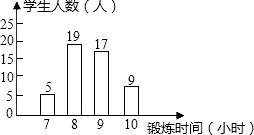 阳光体育运动,要求学生每一天锻炼一小时,如图是依据某班40名同学一周的体育锻炼时间绘制的条形统计图,那么关于该班50名同学一周参加体育锻炼时间的中位数为9小时.
阳光体育运动,要求学生每一天锻炼一小时,如图是依据某班40名同学一周的体育锻炼时间绘制的条形统计图,那么关于该班50名同学一周参加体育锻炼时间的中位数为9小时.