题目内容
 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OA于D,G,交OB于点E,连接DE并延长DE交AB于F,且DE⊥AB
如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OA于D,G,交OB于点E,连接DE并延长DE交AB于F,且DE⊥AB(1)求证:直线AB是⊙O的切线;
(2)若DE=2EF,AB=4
| 3 |
考点:切线的判定,扇形面积的计算
专题:
分析:(1)连接OE,由OA=OB,CA=CB,根据等腰三角形的性质得到OC⊥AB,根据切线的判定定理即可得到结论;
(2)过O点作OH⊥ED于H,则EH=DH,由E=2FE,得到DH=
DF,又因为OH∥BA,根据平行线分线段成比例定理得到DH:DF=DO:DA,AO=2OD,则OB=2OC,得到∠B=30°,而BC=
AB=2
,利用含30°的直角三角形三边的关系得到OC=
BC=2,然后根据三角形和扇形的面积公式利用S阴影部分=S△OAB-S扇形OEG计算即可.
(2)过O点作OH⊥ED于H,则EH=DH,由E=2FE,得到DH=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
解答: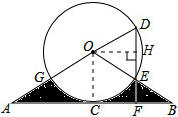 (1)证明:连接OC,如图,
(1)证明:连接OC,如图,
∵OA=OB,CA=CB,
∴OC⊥AB,
∴直线AB是⊙O的切线;
(2)解:过O点作OH⊥ED于H,如图,
∵OE=OD,
∴EH=DH,
∵ED=2EF,
∴DH=
DF,
而DF⊥AB,
∴OH∥BA,
∴DH:DF=DO:DA,
∴AO=2OD,
∴OB=2OC,
∴∠B=30°,∠COB=60°
而BC=
AB=2
,
∴OC=
BC=2,
∴S阴影部分=S△OAB-S扇形OEG
=
•4
•2-
=4
-
π.
 (1)证明:连接OC,如图,
(1)证明:连接OC,如图,∵OA=OB,CA=CB,
∴OC⊥AB,
∴直线AB是⊙O的切线;
(2)解:过O点作OH⊥ED于H,如图,
∵OE=OD,
∴EH=DH,
∵ED=2EF,
∴DH=
| 1 |
| 3 |
而DF⊥AB,
∴OH∥BA,
∴DH:DF=DO:DA,
∴AO=2OD,
∴OB=2OC,
∴∠B=30°,∠COB=60°
而BC=
| 1 |
| 2 |
| 3 |
∴OC=
| ||
| 3 |
∴S阴影部分=S△OAB-S扇形OEG
=
| 1 |
| 2 |
| 3 |
| 120•π•22 |
| 360 |
| 3 |
| 4 |
| 3 |
点评:本题考查了切线的判定定理:过半径的外端点与半径垂直的直线是圆的切线.也考查了扇形的面积公式以及三角形相似的判定与性质.

练习册系列答案
相关题目
下列运算错误的是( )
| A、(-a)(-a)=(-a)2 |
| B、-32•(-3)4=(-3)6 |
| C、(-a)3•(-a)2=(-a)5 |
| D、(-a)3•(-a)3=a6 |
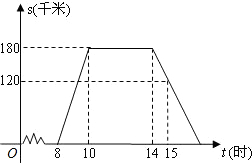 “国庆黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的折线表示.根据图象提供的有关信息,解答下列问题:
“国庆黄金周”的某一天,小明全家上午8时自驾小汽车从家里出发,到距离180千米的某著名旅游景点游玩.该小汽车离家的距离s(千米)与时间t(时)的关系可以用图中的折线表示.根据图象提供的有关信息,解答下列问题:
 如图①,△ABC是等边三角形,D是BC边上的一点(点D与B、C两点不重合),连接AD,以AD为一边向右侧作等边三角形△ADE,连接CE.
如图①,△ABC是等边三角形,D是BC边上的一点(点D与B、C两点不重合),连接AD,以AD为一边向右侧作等边三角形△ADE,连接CE.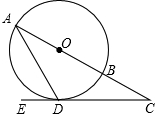 如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.
如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°. 如图,点G是线段EF的中点,则EG=
如图,点G是线段EF的中点,则EG=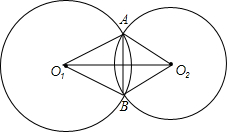 如图,⊙O1与⊙O2相交于A,B两点,连接O1A,O1B,O2A,O2B,得到四边形O1AO2B,连接O1O2,则O1O2垂直平分AB,请说明理由.
如图,⊙O1与⊙O2相交于A,B两点,连接O1A,O1B,O2A,O2B,得到四边形O1AO2B,连接O1O2,则O1O2垂直平分AB,请说明理由.