题目内容
15．多项式x2+mx+6因式分解得（x-2）（x+n），则m=-5．分析 根据因式分解是把一个多项式转化成几个整式积，可得答案．
解答 解：x2+mx+6因式分解得（x-2）（x+n），得
x2+mx+6=（x-2）（x+n），（x-2）（x+n）=x2+（n-2）x-2n，
x2+mx+6=x2+（n-2）x-2n，
-2n=6，m=n-2．
解得n=-3，m=-5，
故答案为：-5．
点评 本题考查了因式分解的意义，利用因式分解得出相等整式是解题关键．
练习册系列答案
相关题目
3．在-$\sqrt{4}$，3.14，π，$\sqrt{10}$，1.$\stackrel{•}{5}\stackrel{•}{1}$，$\frac{2}{7}$，$\root{3}{8}$中，无理数的个数是（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
4．
如图，将弧$\widehat{AB}$沿AB弦折叠，圆弧恰好经过圆心O，弦AD与弧$\widehat{AB}$交于点C，连接BC，则下列结论错误的是（ ）
如图，将弧$\widehat{AB}$沿AB弦折叠，圆弧恰好经过圆心O，弦AD与弧$\widehat{AB}$交于点C，连接BC，则下列结论错误的是（ ）| A． | AC：BC=2：3 | B． | ∠BCD=60° | ||
| C． | BC=CD | D． | 优弧是劣弧长的2倍 |
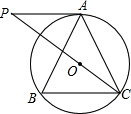如图，⊙O是△ABC的外接圆，AB=AC，连接CO并延长交⊙O的切线AP于点P．