题目内容
19.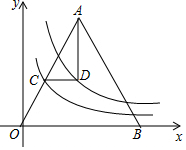 如图,在△OAB中,AO=AB,S△AOB=10,函数y=$\frac{k}{x}$(x>0)图象与OA交于点C,点D是函数y=$\frac{4}{x}$(x>0)的图象上一点,且CD∥x轴,若∠ADC=90°,则k的值是$\frac{8}{5}$.
如图,在△OAB中,AO=AB,S△AOB=10,函数y=$\frac{k}{x}$(x>0)图象与OA交于点C,点D是函数y=$\frac{4}{x}$(x>0)的图象上一点,且CD∥x轴,若∠ADC=90°,则k的值是$\frac{8}{5}$.
分析 过点C作CE⊥x轴于点E,延长AD,交x轴于点F,连接OD,由等腰三角形的性质可得出S△AOF=$\frac{1}{2}$S△AOB=5,利用反比例函数系数k的几何意义可得出S△OCE=$\frac{1}{2}$k、S△ODF=$\frac{1}{2}$×4=2,再由△ODF和△OAF等高可得出$\frac{DF}{AF}$=$\frac{2}{5}$,利用相似三角形的判定与性质可得出S△OCE的值,进而即可求出k值,此题得解.
解答 解:过点C作CE⊥x轴于点E,延长AD,交x轴于点F,连接OD,如图所示.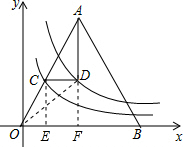
∵AO=AB,CD∥x轴,∠ADC=90°,
∴AF⊥OB,
∴S△AOF=$\frac{1}{2}$S△AOB=5.
∵函数y=$\frac{k}{x}$(x>0)图象与OA交于点C,点D是函数y=$\frac{4}{x}$(x>0)的图象上一点,
∴S△OCE=$\frac{1}{2}$k,S△ODF=$\frac{1}{2}$×4=2,
∴$\frac{DF}{AF}$=$\frac{{S}_{△ODF}}{{S}_{△AOF}}$=$\frac{2}{5}$.
∵CE⊥x轴,AF⊥x轴,CD∥x轴,
∴△OCE∽△OAF,CE=DF,
∴$\frac{{S}_{OCE}}{{S}_{△AOF}}$=$(\frac{DF}{AF})^{2}$,
∴S△OCE=$\frac{1}{2}$k=($\frac{2}{5}$)2×5=$\frac{4}{5}$,
∴k=$\frac{8}{5}$.
故答案为:$\frac{8}{5}$.
点评 本题考查了反比例函数系数k的几何意义、等腰三角形的性质以及相似三角形的判定与性质,利用相似三角形的性质求出S△OCE的值是解题的关键.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案
| A. | 20 | B. | 24 | C. | 48 | D. | 60 |
| A. | 10×108 | B. | 0.1×1010 | C. | 1×109 | D. | 1×1010 |
| A. | x≠0 | B. | x≥0 | C. | x≠9 | D. | x≥9 |
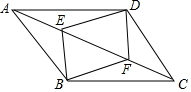 已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:EB∥DF.
已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:EB∥DF.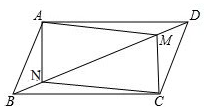 如图,BD是?ABCD的一条对角线,且△ABN与△ADM的面积相等.
如图,BD是?ABCD的一条对角线,且△ABN与△ADM的面积相等.