题目内容
6. 如图,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=$\frac{3}{5}$.
如图,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象相交于A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,-4),连接AO,AO=5,sin∠AOC=$\frac{3}{5}$.(1)求反比例函数的解析式;
(2)连接OB,求△AOB的面积;
(3)请直接写出当x<m时,y2的取值范围.
分析 (1)过点A作AE⊥x轴于点E,在Rt△AEO中,通过解直角三角形可求出点A的坐标,由反比例函数图象上点的坐标特征即可求出反比例函数的解析式;
(2)由反比例函数图象上点的坐标特征可求出点B的坐标,根据点A、B的坐标,利用待定系数法可求出直线AB的解析式,再根据一次函数图象上点的坐标特征可求出点C的坐标,利用三角形的面积公式即可求出△AOB的面积;
(3)观察函数图象可得出:x<0以及0<x<3时,y2的取值范围,合在一起即可得出结论.
解答 解:(1)过点A作AE⊥x轴于点E,如图所示.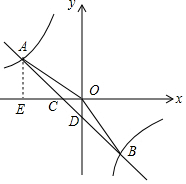
在Rt△AEO中,AO=5,sin∠AOC=$\frac{3}{5}$,
∴AE=AO•sin∠AOC=5×$\frac{3}{5}$=3,
∴OE=$\sqrt{A{O}^{2}-A{E}^{2}}$=4,
∴点A的坐标为(-4,3).
∵点A在反比例函数y2=$\frac{{k}_{2}}{x}$的图象上,
∴k2=-4×3=-12,
∴反比例函数的解析式为y2=-$\frac{12}{x}$.
(2)∵点B(m,-4)反比例函数y2=-$\frac{12}{x}$的图象上,
∴-4=-$\frac{12}{m}$,解得:m=3,
∴点B的坐标为(3,-4).
将A(-4,3)、B(3,-4)代入y1=k1x+b中,
$\left\{\begin{array}{l}{-4{k}_{1}+b=3}\\{3{k}_{1}+b=-4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=-1}\\{b=-1}\end{array}\right.$,
∴直线AB的解析式为y=-x-1.
当y=-x-1=0时,x=-1,
∴点C的坐标为(-1,0),
∴S△AOB=$\frac{1}{2}$OC•(yA-yB)=$\frac{1}{2}$×1×[3-(-4)]=$\frac{7}{2}$.
(3)观察函数图象可知:当x<0时,y2>0;当0<x<3时,y2<-4.
∴当x<3时,y2>0或y2<-4.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求一次函数解析式、反比例(一次)函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)通过解直角三角形找出点A的坐标;(2)根据点A、B的坐标,利用待定系数法求出直线AB的解析式;(3)观察函数图象,找出当x<m时,y2的取值范围.

| A. | $\frac{1}{x-1}$ | B. | $\frac{1}{1-x}$ | C. | $\frac{5}{1-x}$ | D. | $\frac{5}{x-1}$ |
| A. | 7.44×105 | B. | 0.744×106 | C. | 744×103 | D. | 7.11×106 |
 如图,点D是△ABC的边AB上的一点,DE∥BC交AC于点E,作DF∥AC交BC于点F,分别记△ADE,△BDF,?DFCE,△ABC的面积为S1,S2,S3,S有以下结论:
如图,点D是△ABC的边AB上的一点,DE∥BC交AC于点E,作DF∥AC交BC于点F,分别记△ADE,△BDF,?DFCE,△ABC的面积为S1,S2,S3,S有以下结论:
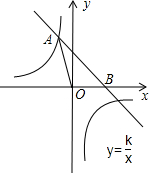 如图,已知直线y=-x+4与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,a),并且与x轴相交于点B.
如图,已知直线y=-x+4与反比例函数y=$\frac{k}{x}$的图象相交于点A(-2,a),并且与x轴相交于点B.