题目内容
不等式﹣2x＜4的解集是（ ）
A. x＞2 B. x＜2 C. x＜﹣2 D. x＞﹣2
D
【解析】两边同时除以﹣2，得：x＞﹣2．
故选D．
黄冈创优卷系列答案“五•四”青年节，市团委组织部分中学的团员去西山植树．某校九年级（3）班团支部领到一批树苗，若每人植4棵树，还剩37棵；若每人植6棵树，则最后一人有树植，但不足3棵，这批树苗共有__棵．
121
【解析】【解析】
设市团委组织部分中学的团员有x人，则树苗有（4x+37）棵，由题意得：
1≤（4x+37）﹣6（x﹣1）＜3
去括号得：1≤﹣2x+43＜3，
移项得：﹣42≤﹣2x＜﹣40，
解得：20＜x≤21．
∵x取正整数，∴x=21，
当x=21时，4x+37=4×21+37=121，则共有树苗4×21+37=121棵．
故答案... 小明身高1.5米，小明爸爸身高1.8米，小明走上一处每级高a米，共10级的平台说：“爸爸，现在两个你的身高都比不上我了！”由此可得关于a的不等式是（ ）
A. 10a＞1.8×2 B. 1.5+a+10＞1.8×2 C. 10a+1.5＞1.8×2 D. 1.8×2＞10a+15
C
【解析】根据小明的身高+10级高台的高度＞爸爸身高的2倍列式即可．
【解析】
根据题意，得10a+1.5＞1.8×2．
故选：C． 不等式组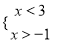
的解集是_________．
﹣1＜x＜3
【解析】根据“小大大小中间找”的原则求出不等式组的解集即可．
∵﹣1＜3，
∴此不等式组的解集为：﹣1＜x＜3．
故答案为：﹣1＜x＜3． 要使代数式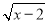
有意义,则x的取值范围是( )
A.x≥2 B.x≥-2 C.x≤-2 D.x≤2
A．
【解析】
试题分析：根据题意，得
x-2≥0，
解得，x≥2；
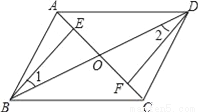
故选A． 如图，四边形ABCD中，对角线AC，BD相交于点O，点E，F分别在OA，OC上
（1）给出以下条件；①OB=OD，②∠1=∠2，③OE=OF，请你从中选取两个条件证明△BEO≌△DFO；
（2）在（1）条件中你所选条件的前提下，添加AE=CF，求证：四边形ABCD是平行四边形．
（1）见解析；（2）见解析.
【解析】试题分析：（1）选取①②，利用ASA判定△BEO≌△DFO；也可选取②③，利用AAS判定△BEO≌△DFO；还可选取①③，利用SAS判定△BEO≌△DFO；
（2）根据△BEO≌△DFO可得EO＝FO，BO＝DO，再根据等式的性质可得AO＝CO，根据两条对角线互相平分的四边形是平行四边形可得结论．
试题解析：
证明：（1）选取①②，
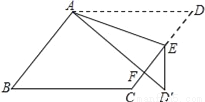
... 如图，在?ABCD中，E为边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F．若∠B=52°，∠DAE=20°，则∠FED′的大小为________．
36°
【解析】试题分析：∵四边形ABCD是平行四边形，
∴∠D＝∠B＝52°，
由折叠的性质得：∠D′＝∠D＝52°，∠EAD′＝∠DAE＝20°，
∴∠AEF＝∠D＋∠DAE＝52°＋20°＝72°，∠AED′＝180°－∠EAD′－∠D′＝108°，
∴∠FED′＝108°－72°＝36°；
故答案为：36°． 如图，□ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N。
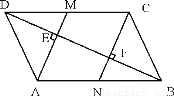
（1）求证：四边形CMAN是平行四边形。
（2）已知DE＝4，FN＝3，求BN的长。
（1）详见解析；（2）5．
【解析】
试题分析：（1）通过AE⊥BD，CF⊥BD证明AE∥CF，再由四边形ABCD是平行四边形得到AB∥CD，由两组对边分别平行的四边形是平行四边形可证得四边形CMAN是平行四边形；（2）证明△MDE≌∠NBF，根据全等三角形的性质可得DE=BF=4，再由勾股定理得BN=5．
试题解析：（1）证明：∵AE⊥BD CF⊥BD
∴AE∥CF
... 如图，在四边形ABCD中，对角线AC，BD相交于点E，∠CBD＝90°，BC＝4，BE＝ED＝3，AC＝10，则四边形ABCD的面积为( )
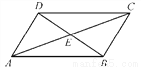
A. 6 B. 12 C. 20 D. 24
D
【解析】试题分析：在Rt△CBE中，由勾股定理可求得EC=5，又因AC=10，所以AE=EC=5.根据对角线互相平分的四边形是平行四边形可判定四边形ABCD是平行四边形，所以平行四边形ABCD的面积为BC×BD=4×6=24，故答案选D.