题目内容
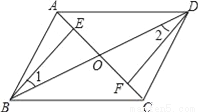
如图，四边形ABCD中，对角线AC，BD相交于点O，点E，F分别在OA，OC上
（1）给出以下条件；①OB=OD，②∠1=∠2，③OE=OF，请你从中选取两个条件证明△BEO≌△DFO；
（2）在（1）条件中你所选条件的前提下，添加AE=CF，求证：四边形ABCD是平行四边形．
（1）见解析；（2）见解析.
【解析】试题分析：（1）选取①②，利用ASA判定△BEO≌△DFO；也可选取②③，利用AAS判定△BEO≌△DFO；还可选取①③，利用SAS判定△BEO≌△DFO；
（2）根据△BEO≌△DFO可得EO＝FO，BO＝DO，再根据等式的性质可得AO＝CO，根据两条对角线互相平分的四边形是平行四边形可得结论．
试题解析：
证明：（1）选取①②，
...
练习册系列答案
相关题目
甲种蔬菜保鲜适宜的温度是1℃～5℃，乙种蔬菜保鲜适宜的温度是3℃～8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是（ ）
A. 1℃～3℃ B. 3℃～5℃ C. 5℃～8℃ D. 1℃～8℃
B
【解析】试题分析：设温度为x℃，由题意得，解得3≤x≤5，故答案选B. 是否存在整数k，使方程组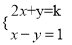
的解中，x大于1，y不大于1，若存在，求出k的值，若不存在，说明理由．
k只能取3，4，5
【解析】【试题分析】解此题时可以解出二元一次方程组中x，y关于k的式子，然后解出k的范围，即可知道k的取值．
【试题解析】解方程组得
∵x大于1，y不大于1从而得不等式组
解之得2＜k≤5
又∵k为整数
∴k只能取3，4，5
答：当k为3，4，5时，方程组的解中，x大于1，y不大于1． 若a＞b＞0，则下列结论正确的是（ ）
A. ﹣a＞﹣b B.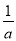 
＞
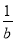C. a3＜0 D. a2＞b2
D
【解析】A、不等式两边都乘﹣1，不等号的方向改变，错误；
B、3＞2＞0，但＜，错误；
C、正数的奇次幂是正数，a3＞0，错误；
D、两个正数，较大的数的平方也大，正确；
故选D. 不等式﹣2x＜4的解集是（ ）
A. x＞2 B. x＜2 C. x＜﹣2 D. x＞﹣2
D
【解析】两边同时除以﹣2，得：x＞﹣2．
故选D． 如图，在四边形ABCD中，AB∥DC，E是AD中点，EF⊥BC于点F，BC=5，EF=3．
（1）若AB=DC，则四边形ABCD的面积S=__；
（2）若AB＞DC，则此时四边形ABCD的面积S′__S（用“＞”或“=”或“＜”填空）．
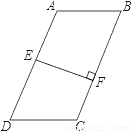
(1)15；（2）=．
【解析】试题分析：（1）∵AB=DC，AB∥DC，
∴四边形ABCD是平行四边形，
∴四边形ABCD的面积S=5×3=15，
（2）如图，连接EC，延长CD、BE交于点P，
∵E是AD中点，
∴AE=DE，
又∵AB∥CD，
∴∠ABE=∠P，∠A=∠PDE，
在△ABE和△DPE中，
∵，
∴△ABE≌△D... 如图，DE是△ABC的中位线，过点C作CF∥BD交DE的延长线于点F，则下列结论正确的是（ ）
A. EF=CF B. EF=DE C. CF＜BD D. EF＞DE
B
【解析】试题分析：∵DE是△ABC的中位线，
∴DE∥BC，DE＝BC，
∵CF∥BD，
∴四边形BCFD是平行四边形，
∴DF＝BC，CF＝BD，
∴EF＝DF－DE＝BC－DE＝BC＝DE．
故选B． 如图，E是?ABCD的边CD的中点，延长AE交BC的延长线于点F．
（1）求证：△ADE≌△FCE．
（2）若∠BAF=90°，BC=5，EF=3，求CD的长．
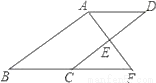
（1）证明过程见解析；（2）8.
【解析】试题分析：（1）由平行四边形的性质得出AD∥BC，AB∥CD，证出∠DAE=∠F，∠D=∠ECF，由AAS证明△ADE≌△FCE即可；（2）由全等三角形的性质得出AE=EF=3，由平行线的性质证出∠AED=∠BAF=90°，由勾股定理求出DE，即可得出CD的长．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AD∥BC，AB∥CD，
... 如图，在平行四边形ABCD中，∠ABC的平分线交AD于E，∠BED=150°，则∠A的大小为（ ）
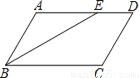
A. 150° B. 130° C. 120° D. 100°
C
【解析】试题分析：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠AEB=∠CBE，∵BE平分∠ABE，∴∠ABE=∠CBE，∴∠AEB=∠ABE，∴AB=AE，∵∠BED=150°，∴∠ABE=∠AEB=30°，∴∠A=180°﹣∠ABE﹣∠AEB=120°．故选C．