��Ŀ����
��ͼ����?ABCD�У�EΪ��CD��һ�㣬����ADE��AE�۵�����AD��E����AD����CE���ڵ�F������B=52�㣬��DAE=20�㣬���FED��Ĵ�СΪ________��
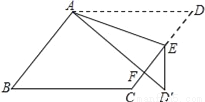
 36��
��������������������ı���ABCD��ƽ���ı��Σ�
���D����B��52�㣬
���۵������ʵã���D�䣽��D��52�㣬��EAD�䣽��DAE��20�㣬
���AEF����D����DAE��52�㣫20�㣽72�㣬��AED�䣽180�㣭��EAD�䣭��D�䣽108�㣬
���FED�䣽108�㣭72�㣽36�㣻
�ʴ�Ϊ��36�㣮
36��
��������������������ı���ABCD��ƽ���ı��Σ�
���D����B��52�㣬
���۵������ʵã���D�䣽��D��52�㣬��EAD�䣽��DAE��20�㣬
���AEF����D����DAE��52�㣫20�㣽72�㣬��AED�䣽180�㣭��EAD�䣭��D�䣽108�㣬
���FED�䣽108�㣭72�㣽36�㣻
�ʴ�Ϊ��36�㣮
�������ʽax��4��0�Ľ⼯�������ϱ�ʾ��ͼ����ôa��ֵΪ____.

 -2
���������ⲻ��ʽax��4��0�ã� �������Ͽɵã�����ʽ�Ľ⼯Ϊ�� ,�� ��ã� .
�ʴ�Ϊ
-2
���������ⲻ��ʽax��4��0�ã� �������Ͽɵã�����ʽ�Ľ⼯Ϊ�� ,�� ��ã� .
�ʴ�Ϊ ������ʽ�� �н⣬��a��ȡֵ��Χ��__________________.
�н⣬��a��ȡֵ��Χ��__________________.
 a��2
����������x��2��x��a��Ҫʹ2���й�������,�������㣺a��2.
��a��ȡֵ��Χ��a��2.
a��2
����������x��2��x��a��Ҫʹ2���й�������,�������㣺a��2.
��a��ȡֵ��Χ��a��2. ����ʽ��2x��4�Ľ⼯�ǣ�������
A. x��2 B. x��2 C. x����2 D. x����2
 D
������������ͬʱ���ԩ�2���ã�x����2��
��ѡD��
D
������������ͬʱ���ԩ�2���ã�x����2��
��ѡD�� ��ͼ����?ABCD�У�E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F��
��1����֤��AB=CF��
��2������DE����AD=2AB����֤��DE��AF��
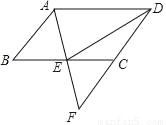
 ��1��֤����������2��֤��������
�������������������1������?ABCD�У�E��BC���е㣬����ASA�������ж���ABE�ա�FCE���̶�֤�ý��ۣ���2����AD=2AB��AB=FC=CD���ɵ�AD=DF�����ɡ�ABE�ա�FCE���ɵ�AE=EF��Ȼ���������ߺ�һ��֤�ý��ۣ�
�����������1�����ı���ABCD��ƽ���ı��Σ� ��AB��DF�� ���ABE=��FCE�� ��EΪBC�е㣬 ��BE=C...
��1��֤����������2��֤��������
�������������������1������?ABCD�У�E��BC���е㣬����ASA�������ж���ABE�ա�FCE���̶�֤�ý��ۣ���2����AD=2AB��AB=FC=CD���ɵ�AD=DF�����ɡ�ABE�ա�FCE���ɵ�AE=EF��Ȼ���������ߺ�һ��֤�ý��ۣ�
�����������1�����ı���ABCD��ƽ���ı��Σ� ��AB��DF�� ���ABE=��FCE�� ��EΪBC�е㣬 ��BE=C... ��ͼ��DE�ǡ�ABC����λ�ߣ�����C��CF��BD��DE���ӳ����ڵ�F�������н�����ȷ���ǣ�������

A. EF=CF B. EF=DE C. CF��BD D. EF��DE
 B
�������������������DE�ǡ�ABC����λ�ߣ�
��DE��BC��DE��BC��
��CF��BD��
���ı���BCFD��ƽ���ı��Σ�
��DF��BC��CF��BD��
��EF��DF��DE��BC��DE��BC��DE��
��ѡB��
B
�������������������DE�ǡ�ABC����λ�ߣ�
��DE��BC��DE��BC��
��CF��BD��
���ı���BCFD��ƽ���ı��Σ�
��DF��BC��CF��BD��
��EF��DF��DE��BC��DE��BC��DE��
��ѡB�� ��ͼ��һ����5��ֽƬƴ�ɵ�ƽ���ı��Σ�����ֽƬ֮�以���ص�Ҳ��϶���������ŵ���ֱ��������ֽƬ�������ΪS1��������ֱ��������ֽƬ�������ΪS2���м�һ��������ֽƬ�����ΪS3�������ƽ���ı��ε����һ�����Ա�ʾΪ��������
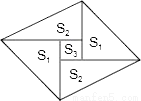
A. 4S1 B. 4S2 C. 4S2+S3 D. 3S1+4S3
 A
����������������������ֱ�������ε�ֱ�DZ߳�Ϊa���м�С�����εı߳�Ϊb����������ֱ�������εı߳��ֱ�Ϊa-b��a+b������S1=��S2=��S3=��ƽ���ı��ε����=2S1+2S2+S3=++=2=4S1���ʴ�ѡA.
A
����������������������ֱ�������ε�ֱ�DZ߳�Ϊa���м�С�����εı߳�Ϊb����������ֱ�������εı߳��ֱ�Ϊa-b��a+b������S1=��S2=��S3=��ƽ���ı��ε����=2S1+2S2+S3=++=2=4S1���ʴ�ѡA. ��ͼ����A��BΪ���㣬��ֱ��l//AB��P��l��һ���㣮��M��N�ֱ�ΪPA��PB���е㣬�������и�ֵ��
���߶�MN�ij���
�ڡ�PAB���ܳ���
�ۡ�PMN�������
��ֱ��MN��AB֮��ľ��룻
�ݡ�APB�Ĵ�С��
���л����P���ƶ����仯���ǣ� ��
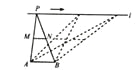
A. �ڢ� B. �ڢ� C. �٢ۢ� D. �ܢ�
 B
�����������������
�١�MN=AB������MN�ij��Ȳ��䣻
�ڡ��ܳ�C��PAB=��AB+PA+PB�����仯��
�ۡ����S��PMN=S��PAB=��AB��h������hΪֱ��l��AB֮��ľ��룬����;
�ܡ�ֱ��NM��AB֮��ľ������ֱ��l��AB֮��ľ����һ�룬���Բ��䣻
�ݡ�������������λ�ã��۲�ͼ�Σ���֪��APB�Ĵ�С�ڱ仯��
��ѡ��B
B
�����������������
�١�MN=AB������MN�ij��Ȳ��䣻
�ڡ��ܳ�C��PAB=��AB+PA+PB�����仯��
�ۡ����S��PMN=S��PAB=��AB��h������hΪֱ��l��AB֮��ľ��룬����;
�ܡ�ֱ��NM��AB֮��ľ������ֱ��l��AB֮��ľ����һ�룬���Բ��䣻
�ݡ�������������λ�ã��۲�ͼ�Σ���֪��APB�Ĵ�С�ڱ仯��
��ѡ��B ��ͼ�����κ���y=��x+2��2+m��ͼ����y�ύ�ڵ�C����B���������ϣ������C���������ߵĶԳ���Գƣ���֪һ�κ���y=kx+b��ͼ���ö��κ���ͼ���ϵĵ�A����1��0������B��
��1������κ�����һ�κ����Ľ���ʽ��
��2������ͼ��д�����㣨x+2��2+m��kx+b��x��ȡֵ��Χ��
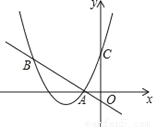
 ��1�������߽���ʽΪy=x2+4x+3��һ�κ�������ʽΪy=��x��1����2����ͼ���֪�����㣨x+2��2+m��kx+b��x��ȡֵ��ΧΪx?��4��x�ݩ�1��
����������1�������ô���ϵ���������m���������B���꣬���÷��������̫�����ǽ���ʽ��
��2�����ݶ��κ�����ͼ����һ�κ�����ͼ�����漴��д���Ա���x��ȡֵ��Χ��
��������
��1����������y=��x+2��2+m������A����1��0...
��1�������߽���ʽΪy=x2+4x+3��һ�κ�������ʽΪy=��x��1����2����ͼ���֪�����㣨x+2��2+m��kx+b��x��ȡֵ��ΧΪx?��4��x�ݩ�1��
����������1�������ô���ϵ���������m���������B���꣬���÷��������̫�����ǽ���ʽ��
��2�����ݶ��κ�����ͼ����һ�κ�����ͼ�����漴��д���Ա���x��ȡֵ��Χ��
��������
��1����������y=��x+2��2+m������A����1��0... 
