题目内容
泰州某地方特产黄桥烧饼专卖店平均每天可卖出400个烧饼,卖出1个烧饼可盈利1.5元.经调查发现,零售单价每降0.1元,该店平均每天可多卖出100个烧饼.为了使每天盈利更多,该店决定把零售单价下降x(0<x<1.5)元.求:
(1)零售单价下降0.2元后,平均每天盈利多少元?
(2)在不考虑其他因素的条件下,当x定为多少时,才能使该店每天盈利900元?
(1)零售单价下降0.2元后,平均每天盈利多少元?
(2)在不考虑其他因素的条件下,当x定为多少时,才能使该店每天盈利900元?
考点:一元二次方程的应用
专题:销售问题
分析:(1)求出下降0.2元后,卖出的数量,以及每个利润,得到平均每天得盈利即可;
(2)根据题意列出方程,求出方程的解即可得到结果.
(2)根据题意列出方程,求出方程的解即可得到结果.
解答:解:(1)下降0.2元后,卖出400+200=600(个)烧饼,每个利润为1.5=0.2=1.3(元),
则每天利润为600×1.3=780元;
(2)由题意得:(1.5-x)(400+
x)=900,
化简得:10x2-11x+3=0,
解得:x1=0.5,x2=0.6,
答:当x定为0.5元或0.6元时,才能使该店每天盈利900元.
则每天利润为600×1.3=780元;
(2)由题意得:(1.5-x)(400+
| 100 |
| 0.1 |
化简得:10x2-11x+3=0,
解得:x1=0.5,x2=0.6,
答:当x定为0.5元或0.6元时,才能使该店每天盈利900元.
点评:此题考查了一元二次方程的应用,弄清题意是解本题的关键.

练习册系列答案
相关题目
一次函数y=x+5的图象经过点P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值为( )
| A、9 | B、-16 |
| C、25 | D、-25. |
 在如图的方格纸中,每个小方格都是边长为1个单位的正方形,建立平面直角坐标系(如图),在同一平面直角坐标系中有5个点:(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(0,-3).
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,建立平面直角坐标系(如图),在同一平面直角坐标系中有5个点:(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(0,-3). 如图,直线y=kx-1与x轴、y轴分别交与B、C两点,且OB、OC(OB<OC)分别是一元二次方程2x2-3x+1=0的两根.
如图,直线y=kx-1与x轴、y轴分别交与B、C两点,且OB、OC(OB<OC)分别是一元二次方程2x2-3x+1=0的两根.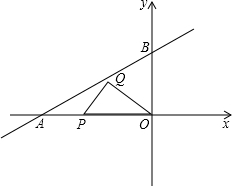 如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),P为线段OA上一个动点,Q为第二象限的一个动点,且满足PQ=PA,OQ=OB.
如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),P为线段OA上一个动点,Q为第二象限的一个动点,且满足PQ=PA,OQ=OB.
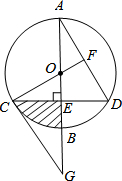 如图,已知⊙O的直径AB垂直弦CD于点E,过C点作⊙O的切线CG交AB延长线于点G,连接CO并延长交AD于点F,且AF=FD.
如图,已知⊙O的直径AB垂直弦CD于点E,过C点作⊙O的切线CG交AB延长线于点G,连接CO并延长交AD于点F,且AF=FD. 已知:如图,直线l的解析式为
已知:如图,直线l的解析式为