题目内容
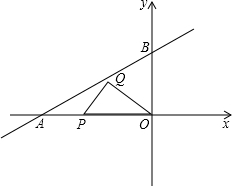 如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),P为线段OA上一个动点,Q为第二象限的一个动点,且满足PQ=PA,OQ=OB.
如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),P为线段OA上一个动点,Q为第二象限的一个动点,且满足PQ=PA,OQ=OB.(1)求直线AB的函数关系式;
(2)若△OPQ为直角三角形,试求点P的坐标,并判断点Q是否在直线AB上.
考点:一次函数综合题
专题:
分析:(1)首先设直线AB的函数关系式为:y=kx+b,由直线AB交x轴于点A(-4,0),交y轴于点B(0,2),利用待定系数法即可求得直线AB的函数关系式;
(2)由△OPQ为直角三角形,则可判定∠PQO=90°,然后设AP=PQ=a,PO=4-a,由勾股定理可得方程:(4-a)2=a2+22,继而求得答案.
(2)由△OPQ为直角三角形,则可判定∠PQO=90°,然后设AP=PQ=a,PO=4-a,由勾股定理可得方程:(4-a)2=a2+22,继而求得答案.
解答:解:(1)设直线AB的函数关系式为:y=kx+b,
∵点A(-4,0),点B(0,2),
∴
,
解得:
,
∴直线AB的函数关系式为:y=
x+2;
(2)∵△OPQ为直角三角形,
①若∠POQ=90°,则点Q在y轴上,
∵Q为第二象限的一个动点,
∴矛盾,
∴∠POQ≠90°;
②若∠QPO=90°,
则PA=PQ<OQ,PO<OQ,
∵OQ=OB=2,PO<2,
∴OA=OP+PA<4,
∵OA=4,
∴矛盾,
∴∠QPO≠90°;
③若∠PQO=90°,设AP=PQ=a,PO=4-a,
∴(4-a)2=a2+22,
解得:a=
,
∴PO=4-a=
,
∴点P的坐标为:(-
,0),
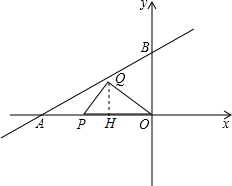
过点Q作QH⊥OP于点H,
∴QH=
=
,
∴OH=
=
,
∴点Q的坐标为:(-
,
);
∵当x=-
时,y=
×(-
)+2=
,
∴点Q在直线AB上.
∵点A(-4,0),点B(0,2),
∴
|
解得:
|
∴直线AB的函数关系式为:y=
| 1 |
| 2 |
(2)∵△OPQ为直角三角形,
①若∠POQ=90°,则点Q在y轴上,
∵Q为第二象限的一个动点,
∴矛盾,
∴∠POQ≠90°;
②若∠QPO=90°,
则PA=PQ<OQ,PO<OQ,
∵OQ=OB=2,PO<2,
∴OA=OP+PA<4,
∵OA=4,
∴矛盾,
∴∠QPO≠90°;
③若∠PQO=90°,设AP=PQ=a,PO=4-a,
∴(4-a)2=a2+22,
解得:a=
| 3 |
| 2 |

∴PO=4-a=
| 5 |
| 2 |
∴点P的坐标为:(-
| 5 |
| 2 |
过点Q作QH⊥OP于点H,
∴QH=
| PQ•OQ |
| OP |
| 6 |
| 5 |
∴OH=
| OQ2-QH2 |
| 8 |
| 5 |
∴点Q的坐标为:(-
| 8 |
| 5 |
| 6 |
| 5 |
∵当x=-
| 8 |
| 5 |
| 1 |
| 2 |
| 8 |
| 5 |
| 6 |
| 5 |
∴点Q在直线AB上.
点评:此题考查了待定系数法求一次函数解析式以及直角三角形的性质.此题难度较大,注意掌握数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
相关题目
直角三角形的斜边与一直角边的比是
:1,且较大的锐角为θ,则sinθ等于( )
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在一次数学考试中,某班第一小组14名学生与全班平均分80的差是2,3,-3,-5,12,14,10,4,-6,4,-11,-7,8,-2,那么这个小组的平均成绩约是( )
| A、90分 | B、82分 |
| C、88分 | D、81.64分 |

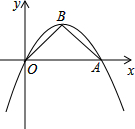 抛物线y=ax2+bx经过点A(4,0),B(2,2),连结OB,AB.
抛物线y=ax2+bx经过点A(4,0),B(2,2),连结OB,AB.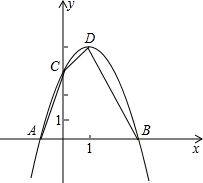 如图,已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)和B(3,0),与y轴交于点C.设抛物线的顶点为D,连结CD、DB、AC.
如图,已知抛物线y=-x2+bx+c与x轴交于点A(-1,0)和B(3,0),与y轴交于点C.设抛物线的顶点为D,连结CD、DB、AC. 如图,已知△ABC
如图,已知△ABC