如图.PA.PB.DE分别切⊙O于A.B.C.DE分别交PA.PB于D.E.已知P到⊙O的切线长为8CM.则△PDE的周长为( )A．16cmB．14cmC．12cmD．8cm 题目和参考答案——青夏教育精英家教网—

题目内容

3．

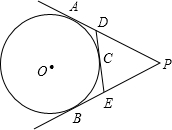如图，PA、PB、DE分别切⊙O于A、B、C，DE分别交PA，PB于D、E，已知P到⊙O的切线长为8CM，则△PDE的周长为（　　）

A．

16cm

B．

14cm

C．

12cm

D．

8cm

分析由切线长定理可知AD=CD、BE=CE，PA=PB，则可求得△PDE的周长=PA+PB，可求得答案．

解答解：
∵PA、PB、DE分别切⊙O于A、B、C，
∴PA=PB=8cm，AD=CD，BE=CE，
∴PD+DE+PE=PD+DC+CE+PE=PD+AD+BE+PE=PA+PB=8+8=16（cm），
故选A．

点评本题主要考查切线长定理，掌握从圆外一点引圆的两条切线所得的切线长相等是解题的关键．

练习册系列答案

14．写出下列命题的逆命题，并判断原命题和逆命题的真假：
（1）若m²≠n²，则m≠n；
（2）如果一个三角形有一个内角是钝角，那么它的另外两个内角是锐角．

11．为了解石柱中学初2017届男生的身高，从中抽取了6名男生，测得身高（单位：cm）为：160，175，170，158，164，157，则这组数据的中位数和极差分别是（　　）

18．若反比例函数y=$\frac{k}{x}$（k≠0）的图象经过点（-1，2），则这个函数的图象一点经过（　　）

8．已知a，b互为相反数，c，d互为倒数，数轴上表示m的点到原点距离为2，求m²+$\frac{a+b}{m}$+cd的值．

15．相切两圆的半径分别为3cm、8cm，则两圆的圆心距是11cm或5cm．

12．已知a=$\frac{1}{\sqrt{2}+1}$，b=$\frac{1}{\sqrt{3}+\sqrt{2}}$，求（a+b）²的值．

13．

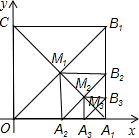如图，在平面直角坐标系中，边长为1的正方形OA₁B₁C的对角线A₁C和OB₁交于点M₁；以A₁M₁为对角线作第二个正方形A₂A₁B₂M₁，对角线A₁M₁和A₂B₂交于点M₂；以A₁M₂为对角线作第三个正方形A₃A₁B₃M₂，对角线A₁M₂和A₃B₃交于点M₃；…依此类推，这样作的第n个正方形对角线交点M_n的坐标是（$\frac{{2}^{n}-1}{{2}^{n}}$，$\frac{1}{{2}^{n}}$）．

试题分类