题目内容
13.一个不透明的口袋中装有2个红球、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.先从中任意摸出1个球,放回捞匀,再任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.分析 画树状图展示所有16种等可能的结果数,再找出两次都摸到红球的结果数,然后根据概率公式求解.
解答 解:画树状图为:
共有16种等可能的结果数,其中两次都摸到红球的结果数为4,
所以两次都摸到红球的概率=$\frac{4}{16}$=$\frac{1}{4}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.\

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
1. 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )
 如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )
如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=12,AC=8,则CD的长为( )| A. | 5.5 | B. | 4 | C. | 4.5 | D. | 3 |
2.已知⊙O的半径为2,点A在直线l上,且AO=2,则直线l与⊙O的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 相切或相交 |
3.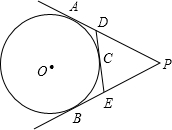 如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则△PDE的周长为( )
如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则△PDE的周长为( )
 如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则△PDE的周长为( )
如图,PA、PB、DE分别切⊙O于A、B、C,DE分别交PA,PB于D、E,已知P到⊙O的切线长为8CM,则△PDE的周长为( )| A. | 16cm | B. | 14cm | C. | 12cm | D. | 8cm |
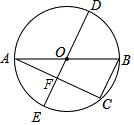 如图,AB是⊙O的直径,AC、BC是⊙O的弦,若点D在优弧ABC上,直径DE⊥AC于点F,AB=8,BC=3,则DF=5.5.
如图,AB是⊙O的直径,AC、BC是⊙O的弦,若点D在优弧ABC上,直径DE⊥AC于点F,AB=8,BC=3,则DF=5.5.