题目内容
已知点P是正方形ABCD的对角线AC上一点.
(1)如图1,求证:PB=PD;
(2)如图2,过点P作PB的垂线,交边CD于点Q,求证△PQD是等腰三角形;
(3)在(2)的条件下,若正方形ABCD的边长为1,AP=
,求△PQD的面积.
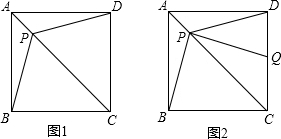
(1)如图1,求证:PB=PD;
(2)如图2,过点P作PB的垂线,交边CD于点Q,求证△PQD是等腰三角形;
(3)在(2)的条件下,若正方形ABCD的边长为1,AP=
| 1 |
| 3 |

考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)根据正方形的性质可得AB=AD,∠BAP=∠DAP,然后利用“边角边”证明△BAP和△DAP全等,根据全等三角形对应边相等证明即可;
(2)根据四边形的内角和等于360°求出∠PBC+∠PQC=180°,然后求出∠PBC=∠PQD,再根据等角的余角相等求出∠PBC=∠PDC,从而得到∠PQD=∠PDC,再根据等角对等边证明即可;
(3)过点P作PM⊥CD于M,作PN⊥AD于N,根据正方形性质求出PM、PN,再求出DQ,然后根据三角形的面积公式列式计算即可得解.
(2)根据四边形的内角和等于360°求出∠PBC+∠PQC=180°,然后求出∠PBC=∠PQD,再根据等角的余角相等求出∠PBC=∠PDC,从而得到∠PQD=∠PDC,再根据等角对等边证明即可;
(3)过点P作PM⊥CD于M,作PN⊥AD于N,根据正方形性质求出PM、PN,再求出DQ,然后根据三角形的面积公式列式计算即可得解.
解答:(1)证明:∵四边形ABCD是正方形,AC为一条对角线,
∴AB=AD,∠BAP=∠DAP,
在△BAP和△DAP中,
,
∴△BAP≌△DAP(SAS),
∴PB=PD;
(2)证明:∵四边形ABCD是正方形,
∴∠BCD=90°,
∵PB⊥PQ,
∴∠PBC+∠PQC=180°,
∵∠PQD+∠PQC=180°,
∴∠PBC=∠PQD,
∵△BAP≌△DAP,
∴∠ABP=∠ADP,
∴∠PBC=∠PDC,
∴∠PQD=∠PDC,
∴PQ=PD;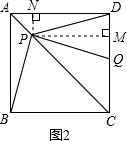
(3)解:如图2,过点P作PM⊥CD于M,作PN⊥AD于N,
∵正方形ABCD的边长为1,AP=
,
∴PN=
×
=
,PM=1-
,
∵PD=PQ,
∴DQ=2MD=2PN=
×2=
,
△PQD的面积=
×
×(1-
)=
.
∴AB=AD,∠BAP=∠DAP,
在△BAP和△DAP中,
|
∴△BAP≌△DAP(SAS),
∴PB=PD;
(2)证明:∵四边形ABCD是正方形,
∴∠BCD=90°,
∵PB⊥PQ,
∴∠PBC+∠PQC=180°,
∵∠PQD+∠PQC=180°,
∴∠PBC=∠PQD,
∵△BAP≌△DAP,
∴∠ABP=∠ADP,
∴∠PBC=∠PDC,
∴∠PQD=∠PDC,
∴PQ=PD;

(3)解:如图2,过点P作PM⊥CD于M,作PN⊥AD于N,
∵正方形ABCD的边长为1,AP=
| 1 |
| 3 |
∴PN=
| 1 |
| 3 |
| ||
| 2 |
| ||
| 6 |
| ||
| 6 |
∵PD=PQ,
∴DQ=2MD=2PN=
| ||
| 6 |
| ||
| 3 |
△PQD的面积=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
3
| ||
| 18 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,等角的余角相等的性质,等腰直角三角形的判定与性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
 如图,下列条件中,不能判断直线a∥b的是( )
如图,下列条件中,不能判断直线a∥b的是( )| A、∠1=∠3 |
| B、∠2=∠3 |
| C、∠4=∠5 |
| D、∠2+∠4=180° |
 如图,在梯形ABCD中,AD∥BC,BD⊥BC,且BD=BC=2AD,点E为AD的中点,连BE,对角线AC分别交BE、BD于点F、G.下列结论:
如图,在梯形ABCD中,AD∥BC,BD⊥BC,且BD=BC=2AD,点E为AD的中点,连BE,对角线AC分别交BE、BD于点F、G.下列结论:
 如图:三角形ABC三个顶点A、B、C的坐标分别为A (1,2)、B(4,3)、C(3,1).
如图:三角形ABC三个顶点A、B、C的坐标分别为A (1,2)、B(4,3)、C(3,1).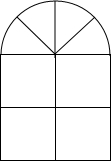 如图,一个窗户的上部是由四个扇形组成的一个半径为R的半圆,下部是边长相同的四个小正方形.
如图,一个窗户的上部是由四个扇形组成的一个半径为R的半圆,下部是边长相同的四个小正方形. 给出如图.
给出如图.