题目内容
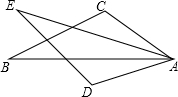
如图、AC、AB是⊙O弦(AB>AC)
(1)如图1,请在AC上确定一点E,使AC2=AE•AB,证明你的结论;
(2)在(1)的结论下延长EC到P,连结PB,若PB=PE,求证:PB是⊙O的切线;
(3)在条件(2)的情况下,若E是PD的中点,那么C是PE的中点吗?若是,请证明;若不是,说明理由.

(1)如图1,请在AC上确定一点E,使AC2=AE•AB,证明你的结论;
(2)在(1)的结论下延长EC到P,连结PB,若PB=PE,求证:PB是⊙O的切线;
(3)在条件(2)的情况下,若E是PD的中点,那么C是PE的中点吗?若是,请证明;若不是,说明理由.

考点:圆的综合题
专题:
分析:(1)能找到一点E,使AC2=AE•AB.当△ACE∽△ABE时就有这个结论;
(2)在条件(1)的结论下,PB和⊙O相切.
如图连接BC,BO,并延长BO交圆与F,连接AF.利用(1)的结论可以得到∠ACB=∠AEC.根据PB=PE,可以得到∠PBE=∠PEB.再利用圆内接四边形的性质和直径所对的圆周角是直角,可以证明∠PBE+∠BAE=90°,从而证明题目结论;
(3)C是PE的中点.根据切线长定理可以得到PB2=PC•PD,而E是PD的中点,可以得到PE=PD,代入PB2=PC•PD中,变换就可以得到题目结论.
(2)在条件(1)的结论下,PB和⊙O相切.
如图连接BC,BO,并延长BO交圆与F,连接AF.利用(1)的结论可以得到∠ACB=∠AEC.根据PB=PE,可以得到∠PBE=∠PEB.再利用圆内接四边形的性质和直径所对的圆周角是直角,可以证明∠PBE+∠BAE=90°,从而证明题目结论;
(3)C是PE的中点.根据切线长定理可以得到PB2=PC•PD,而E是PD的中点,可以得到PE=PD,代入PB2=PC•PD中,变换就可以得到题目结论.
解答: 解:(1)能找到一点E,使AC2=AE•AB.
解:(1)能找到一点E,使AC2=AE•AB.
当∠AEC=∠ACB时,又∵∠A=∠A,
∴△ACE∽△ABE,
∴
=
,
故AC2=AE•AB;
(2)在条件(1)的结论下,PB和⊙O相切.
如图连接BC,BO,并延长BO交圆与F,连接AF.
∵AC2=AE•AB,
∴△ACE∽△ABC.
∴∠ACB=∠AEC,而PB=PE.
∴∠PBE=∠PEB,而∠ACB+∠F=180°,∠AEC+∠PEB=180°,
∴∠F=∠PEB.
∴∠PBE=∠F,而∠F+∠ABF=90°,
∴∠ABF+∠PBE=90°.
∴PB和⊙O相切.
(3)根据(2)可以得到PB2=PC•PD.
而E是PD的中点,可以得到PE=DE.
∴PE2=(PE-CE)×2PE=2PE2-2PE•CE.
∴PE=2CE,
∴C是PE的中点.
 解:(1)能找到一点E,使AC2=AE•AB.
解:(1)能找到一点E,使AC2=AE•AB.当∠AEC=∠ACB时,又∵∠A=∠A,
∴△ACE∽△ABE,
∴
| AC |
| AB |
| AE |
| AC |
故AC2=AE•AB;
(2)在条件(1)的结论下,PB和⊙O相切.
如图连接BC,BO,并延长BO交圆与F,连接AF.
∵AC2=AE•AB,
∴△ACE∽△ABC.
∴∠ACB=∠AEC,而PB=PE.
∴∠PBE=∠PEB,而∠ACB+∠F=180°,∠AEC+∠PEB=180°,
∴∠F=∠PEB.
∴∠PBE=∠F,而∠F+∠ABF=90°,
∴∠ABF+∠PBE=90°.
∴PB和⊙O相切.
(3)根据(2)可以得到PB2=PC•PD.
而E是PD的中点,可以得到PE=DE.
∴PE2=(PE-CE)×2PE=2PE2-2PE•CE.
∴PE=2CE,
∴C是PE的中点.
点评:本题主要考查了圆的切线的判定定理的证明.证明线段的乘积相等的问题一般可以转化为三角形相似问题,证明切线的问题,可以转化为证明切线是垂直于半径,并且经过半径的外端点.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
∑表示数学中的求和符号,主要用于求多个数的和,∑下面的小字,i=1表示从1开始求和;上面的小字,如n表示求和到n为止.即
xi=x1+x2+x3+…+xn.则
(i2-1)表示( )
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| A、n2-1 |
| B、12+22+32+…+i2-i |
| C、12+22+32+…+n2-n |
| D、12+22+32+…+n2-(1+2+3+…+n ) |
某校学生的学习兴趣进行了一次抽样调查(把学生的学习兴趣分为三个层次,A层次:很感兴趣,B层次:较感兴趣,C层次:不感兴趣,并将调查结果绘制成了图①和图②的统计图(不完整),根据图中所给信息估计该校1200名学生中,C层次的学生约有( )


| A、360人 | B、180人 |
| C、30人 | D、1020人 |
一个多边形的每个内角不大于120°.那么这个多边形的边数最多是( )
| A、4 | B、6 | C、8 | D、10 |
 如图,已知∠EAC=∠BAD,AC=AD,增加下列条件:
如图,已知∠EAC=∠BAD,AC=AD,增加下列条件: 在平面直角坐标系中,0为坐标原点,A(-2,3).B (2,2)
在平面直角坐标系中,0为坐标原点,A(-2,3).B (2,2)
 如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:
如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证: 小明把两个大小不相等的等腰直角三角形如图放置(阴影部分),点D在AC上,连接AE、BD.经分析思考后,小明得出如下结论:
小明把两个大小不相等的等腰直角三角形如图放置(阴影部分),点D在AC上,连接AE、BD.经分析思考后,小明得出如下结论: