题目内容
4．已知a2-4a+9b2+6b+5=0，则a+b=$\frac{5}{3}$．分析 利用配方法可得（a-2）2+（3b+1）2=0，根据偶次方的非负性，即可求出a、b的值，将其代入a+b即可得出结论．
解答 解：∵a2-4a+9b2+6b+5=0，
∴（a-2）2+（3b+1）2=0，
∴a=2，b=-$\frac{1}{3}$，
∴a+b=2-$\frac{1}{3}$=$\frac{5}{3}$．
故答案为：$\frac{5}{3}$．
点评 本题考查了配方法的应用以及偶次方的非负性，利用配方法将原式变形为（a-2）2+（3b+1）2=0是解题的关键．
练习册系列答案
新思维寒假作业系列答案
相关题目
已知一次函数y=2x-4．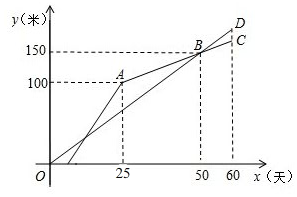
甲、乙两个工程队共同修建一条乡镇公路，甲队按一定的工作效率先施工，一段时间后，乙队从另一端按一定的工作效率加入施工，中途乙队遇到山坡路段，工作效率降低，当乙队完成山坡路段时恰好公路修建完成，此时甲队工作了60天，设甲、乙两队各自修建的公路的长度为y（米），甲队工作时间为x（天），y与x之间的函数图象如图所示．
△ABC在平面直角坐标系xOy中的位置如图所示．