题目内容
12.为便于管理与场地安排,松北某中学校以小明所在班级为例,对学生参加各个体育项目进行了调查统计.并把调查的结果绘制了如图所示的不完全统计图,请你根据下列信息回答问题: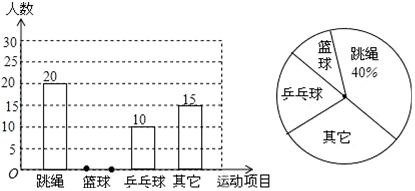
(1)共有50名学生参加了此次调查;
(2)补全条形统计图;
(3)请计算扇形统计图中“乒乓球”所在扇形的圆心角度数;
(4)如果学校有800名学生,请估计全校学生中有多少人参加篮球项目.
分析 (1)用跳绳的人数除以百分比即可得出参加比赛的总人数;
(2)总人数-跳绳人数-乒乓球人数-其它人数=篮球人数;
(3)“乒乓球”所在扇形的圆心角度数=10÷50×360°;
(4)800×(篮球的人数÷总人数).
解答 解:(1)抽查总人数是:20÷40%=50(人),
(2)参加篮球项目的人数是:50-20-10-15=5(人),
即小明所在的班级参加篮球项目的同学有5人,
(3)72°
(4)800×$\frac{5}{50}$=80(人).
答:估计全校学生中大约有80人参加篮球项目.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.也考查了利用样本估计总体.

练习册系列答案
相关题目
12.为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成如表:
(1)上表反映的两个变量中,自变量是t,因变量是Q;
(2)根据上表可知,该车邮箱的大小为100升,每小时耗油6升;
(3)请求出两个变量之间的关系式(用t来表示Q)
| 汽车行驶时间t(小时) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(升) | 100 | 94 | 88 | 82 | … |
(2)根据上表可知,该车邮箱的大小为100升,每小时耗油6升;
(3)请求出两个变量之间的关系式(用t来表示Q)
 如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.
如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.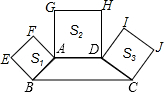 如图,四边形ABCD中,AD∥BC,且∠B+∠C=90°,分别以AB、AD、DC为边向形外作正方形ABEF、正方形ADHG、正方形DCJI,且其面积依次记为S1、S2、S3,若S1+S3=4S2,求$\frac{BC}{AD}$的值.
如图,四边形ABCD中,AD∥BC,且∠B+∠C=90°,分别以AB、AD、DC为边向形外作正方形ABEF、正方形ADHG、正方形DCJI,且其面积依次记为S1、S2、S3,若S1+S3=4S2,求$\frac{BC}{AD}$的值.