题目内容
20.计算:(1)$\frac{2}{{\sqrt{2}-1}}+\sqrt{18}-4\sqrt{\frac{1}{2}}$
(2)$(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})-{(\sqrt{3}-\sqrt{2})^2}$.
分析 (1)首先化简二次根式,进而合并求出答案;
(2)直接利用乘法公式化简二次根式进而得出答案.
解答 解:(1)$\frac{2}{{\sqrt{2}-1}}+\sqrt{18}-4\sqrt{\frac{1}{2}}$
=$\frac{2(\sqrt{2}+1)}{(\sqrt{2}-1)(\sqrt{2}+1)}$+3$\sqrt{2}$-2$\sqrt{2}$
=2$\sqrt{2}$+2+3$\sqrt{2}$-2$\sqrt{2}$
=3$\sqrt{2}$+2;
(2)$(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})-{(\sqrt{3}-\sqrt{2})^2}$
=5-2-(3+2-2$\sqrt{6}$)
=3-5+2$\sqrt{6}$
=-2+2$\sqrt{6}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.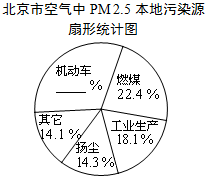 据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:
2014年北京市全年空气质量等级天数统计表
(1)请根据所给信息补全扇形统计图;
(2)请你根据“2014年北京市全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到0.01)
(3)小明是社区环保志愿者,他和同学们调查了本社区的100辆机动车,了解到其中每天出行超过20千米的有40辆.已知北京市2014年机动车保有量已突破520万辆,请你通过计算,估计2014年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物?
 据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:
据报道,历经一年半的调查研究,北京PM 2.5源解析已经通过专家论证.各种调查显示,机动车成为PM 2.5的最大来源,一辆车一天行驶20千米,那么这辆车每天至少就要向大气里排放0.035千克污染物.如图是相关的统计图表:2014年北京市全年空气质量等级天数统计表
| 空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
| 天数(天) | 41 | 135 | 84 | 47 | 45 | 13 |
(2)请你根据“2014年北京市全年空气质量等级天数统计表”计算该年度重度污染和严重污染出现的频率共是多少?(精确到0.01)
(3)小明是社区环保志愿者,他和同学们调查了本社区的100辆机动车,了解到其中每天出行超过20千米的有40辆.已知北京市2014年机动车保有量已突破520万辆,请你通过计算,估计2014年北京市一天中出行超过20千米的机动车至少要向大气里排放多少千克污染物?
10.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.25;(精确到0.01)
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
| 摸到白球的频率$\frac{m}{n}$ | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球;这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.
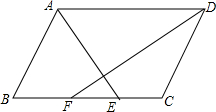 如图,在?ABCD中,AB=4,AD=6,AE、DF分别平分∠BAD、∠ADC,交BC于E、F两点.
如图,在?ABCD中,AB=4,AD=6,AE、DF分别平分∠BAD、∠ADC,交BC于E、F两点.