题目内容
10.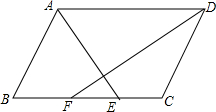 如图,在?ABCD中,AB=4,AD=6,AE、DF分别平分∠BAD、∠ADC,交BC于E、F两点.
如图,在?ABCD中,AB=4,AD=6,AE、DF分别平分∠BAD、∠ADC,交BC于E、F两点.(1)探索AE与DF的位置关系;
(2)试求EF的长.
分析 (1)由在?ABCD中,AE、DF分别平分∠BAD、∠ADC,易求得∠EAD+∠ADF=90°,继而可得AE⊥DF;
(2)易证得△ABE与△CDF是等腰三角形,则可求得BE=CF=AB=4,继而求得答案.
解答  解:(1)AE⊥DF.
解:(1)AE⊥DF.
理由:设AE与DF相较于点M,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAD+∠ADC=180°,
∵AE、DF分别平分∠BAD、∠ADC,
∴∠DAE=$\frac{1}{2}$∠BAD,∠ADF=$\frac{1}{2}$∠ADC,
∴∠DAE+∠ADF=$\frac{1}{2}$(∠BAD+∠ADC)=90°,
∴∠AMD=90°,
即AE⊥DF;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=4,BC=AD=6,
∴∠DAE=∠AEB,∠ADF=∠CFD,
∵AE、DF分别平分∠BAD、∠ADC,
∴∠DAE=∠BAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CDF=∠CFD,
∴AB=BE,CD=CF,
∴BE=CF=4;
∴EF=BE+CF-BC=4+4-6=2.
点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质.注意证得△ABE与△CDF是等腰三角形是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.若不等式(a-1)x≤-3的解集为x≥$\frac{3}{1-a}$,则a的取值范围是( )
| A. | a>1 | B. | a<1 | C. | a>0 | D. | a≤1 |
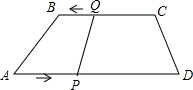 如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P,Q分别从点A,C同时出发,P以1厘米/秒的速度由A向D运动,Q以2厘米/秒的速度由C向B运动.
如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P,Q分别从点A,C同时出发,P以1厘米/秒的速度由A向D运动,Q以2厘米/秒的速度由C向B运动. 如图,已知?ABCD的周长为16cm,AE平分∠BAD交BC于E,设AB=xcm(0<x<4).
如图,已知?ABCD的周长为16cm,AE平分∠BAD交BC于E,设AB=xcm(0<x<4).