题目内容
9．计算：（1）$\root{3}{64}$+$\sqrt{（-3）^{2}}$-$\root{3}{-1}$
（2）$\sqrt{49}$-$\root{3}{27}$+|1-$\sqrt{2}$|+$\sqrt{（1-\frac{5}{4}）^{2}}$．
分析 （1）原式利用立方根，二次根式性质计算即可得到结果；
（2）原式利用算术平方根，立方根，绝对值的代数意义，以及二次根式性质计算即可得到结果．
解答 解：（1）原式=4+3-（-1）=8；
（2）原式=7-3+$\sqrt{2}$-1+$\frac{1}{4}$=3$\frac{1}{4}$+$\sqrt{2}$．
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
19．若不等式（a-1）x≤-3的解集为x≥$\frac{3}{1-a}$，则a的取值范围是（ ）
| A． | a＞1 | B． | a＜1 | C． | a＞0 | D． | a≤1 |
17．
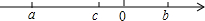已知，三个实数a，b，c在数轴上的点如图所示，|a-b|+|c-a|-|c+b|的值可能是（ ）
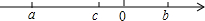已知，三个实数a，b，c在数轴上的点如图所示，|a-b|+|c-a|-|c+b|的值可能是（ ）| A． | 2a | B． | 2b | C． | 2c | D． | -2a |
14．下列各式中最简二次根式为（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{{x}^{2}}$ | C． | $\sqrt{0.7}$ | D． | $\sqrt{\frac{1}{3}}$ |
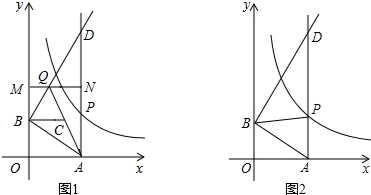
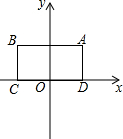对于⊙P及一个矩形给出如下定义：如果⊙P上存在到此矩形四个顶点距离都相等的点，那么称⊙P是该矩形的“等距圆”．如图，在平面直角坐标系xOy中，矩形ABCD的顶点A的坐标为（$\sqrt{3}$，2），顶点C、D在x轴上，且OC=OD．