题目内容
16．方程x2-mx+2m-1=0的两根分别为x1，x2，且-1＜x1＜0，0＜x2＜2，则m的取值范围是0＜m＜$\frac{1}{2}$．分析 由题意设f（x）=x2-mx+2m-1可分三种情况：f（0）＞0，f（-1）＜0，f（2）＞0，解不等式求得实数m的取值范围
解答 解：设f（x）=x2-mx+2m-1，则f（x）=0的根满足-1＜x1＜0，0＜x2＜2，
需要：f（-1）＞0，
则1+m+2m-1＞0，
解得：m＞0；
f（0）＜0，
则2m-1＜0，
解得：m＜$\frac{1}{2}$；
f（2）＞0，
则4-2m+2m-1＞0，
则m的范围是：0＜m＜$\frac{1}{2}$．
故答案为：0＜m＜$\frac{1}{2}$．
点评 本题主要考查一元二次方程根的分布与系数的关系，体现了转化和分类的数学思想
练习册系列答案
相关题目
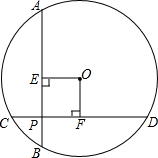如图所示，⊙O的两条弦AB，CD互相垂直且相交于点P，OE⊥AB，OF⊥CD，垂足分别为E，F，$\widehat{AC}$=$\widehat{BD}$．求证：四边形OEPF是正方形．
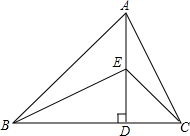已知：如图，AD⊥BC，垂足为D，AD=BD，点E在AD上，∠ABD=∠CED=45°，∠ABE=∠ACE．请写出图中相等的线段，并进行证明．