题目内容
如图,∠1=∠2,添加一个条件使得△ADE∽△ACB .

∠D=∠C或∠E=∠B或 =
=
考点: 相似三角形的判定.
专题: 开放型.
分析: 由∠1=∠2可得∠DAE=∠CAB.只需还有一对角对应相等或夹边对应成比例即可使得△ADE∽△ACB.
解答: 解:∵∠1=∠2,∴∠1+∠BAE=∠2+∠BAE,即∠DAE=∠CAB.
当∠D=∠C或∠E=∠B或 =
= 时,△ADE∽△ACB.
时,△ADE∽△ACB.
点评: 此题考查了相似三角形的判定,属基础题,比较简单.但需注意对应关系.

练习册系列答案
相关题目
 ,AB=3
,AB=3 ,则CD为
,则CD为 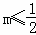
 .
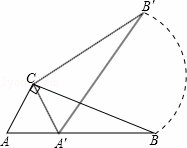
.
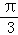 B.
B. 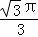 C.
C. 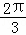 D. π
D. π