题目内容
已知a、b、c是△ABC的三边,且方程b(x2﹣1)﹣2ax+c(x2+1)=0有两个相等的实数根,试判断△ABC的形状.
考点: 一元二次方程的应用.
专题: 几何图形问题.
分析: 根据方程b(x2﹣1)﹣2ax+c(x2+1)=0有两个相等的实数根可知△=0,把对应的值代入△=0中整理即可得到a,b,c之间的关系式,从而可判断三角形的形状.
解答: 解:原方程化为:(b+c)x2﹣2ax﹣b+c=0,
∵方程b(x2﹣1)﹣2ax+c(x2+1)=0有两个相等的实数根,
∴△=(﹣2a)2﹣4(b+c)•(﹣b+c)=4a2﹣4c2+4b2=0
∴a2+b2=c2,即为直角三角形.
点评: 主要考查了一元二次方程的根的判别式的具体运用.一般情况下,知道方程的根的情况后,△经常作为相等或不等关系进行解题.

练习册系列答案
相关题目
 =
= 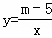 (m为常数)图象的一支.
(m为常数)图象的一支.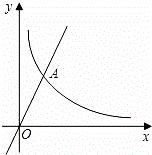
 =
= ×
× C. (3a2)3=9a6 D.
C. (3a2)3=9a6 D.  +
+ =3
=3 ﹣
﹣ +1
+1